如图,在平面直坐标系 中,已知椭圆
中,已知椭圆 ,经过点
,经过点 ,其中e为椭圆的离心率.且椭圆
,其中e为椭圆的离心率.且椭圆 与直线
与直线 有且只有一个交点。
有且只有一个交点。
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设不经过原点的直线 与椭圆
与椭圆 相交与A,B两点,第一象限内的点
相交与A,B两点,第一象限内的点 在椭圆上,直线
在椭圆上,直线 平分线段
平分线段 ,求:当
,求:当 的面积取得最大值时直线
的面积取得最大值时直线 的方程。
的方程。
已知观测点B在A的正西且相距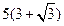 的海面上,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距
的海面上,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距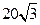 海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
椭圆 :
:
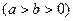 的两个焦点为
的两个焦点为 、
、 ,点
,点 在椭圆
在椭圆 上,且
上,且 ,
, ,
, .
.
(1)求椭圆 的方程;
的方程;
(2)若直线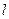 过圆
过圆 的圆心
的圆心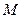 ,交椭圆
,交椭圆 于
于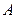 、
、 两点,且
两点,且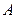 、
、 关于点
关于点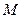 对称,求直线
对称,求直线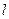 的方程.
的方程.
已知函数
(1)求函数 的最小正周期及单调递减区间
的最小正周期及单调递减区间
(2)当 时,求
时,求 的值域
的值域
已知 ,
, ,且
,且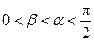 .
.
(Ⅰ)求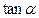 的值;(Ⅱ)求
的值;(Ⅱ)求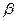 .
.
已知函数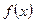 是定义在
是定义在 上的奇函数,并且在
上的奇函数,并且在 上是减函数.是否存在实数
上是减函数.是否存在实数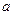 使
使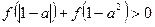 恒成
恒成 立?若存在,求出实数
立?若存在,求出实数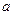 的取值范围;若不存在,请说明理由.[来
的取值范围;若不存在,请说明理由.[来