已知曲线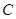 的极坐标方程是
的极坐标方程是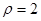 ,以极点为原点,极轴为
,以极点为原点,极轴为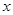 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线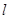 的参数方程为
的参数方程为 (
(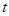 为参数).
为参数).
(1)写出直线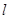 的普通方程与曲线
的普通方程与曲线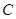 的直角坐标方程;
的直角坐标方程;
(2)设曲线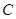 经过伸缩变换
经过伸缩变换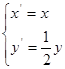 得到曲线
得到曲线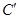 ,设
,设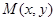 为曲线
为曲线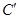 上任一点,求
上任一点,求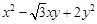 的最小值,并求相应点
的最小值,并求相应点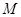 的坐标。
的坐标。
计算: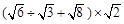
如图,已知△ABC中CE⊥AB于E,BF⊥AC于F,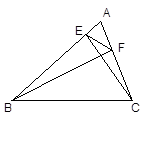
(1)求证:△AFE∽△ABC;
(2)若∠A=60°时 ,求△AFE与△ABC面积之比
已知抛物线 ,
,
(1)用配方法确定它的顶点坐标、对称轴;
(2)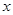 取何值时,
取何值时,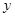 随
随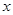 增大而减小?
增大而减小?
(3)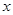 取何值时,抛物线在
取何值时,抛物线在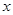 轴上方?
轴上方?
在△ABC中,AB=AC=5,BC=6,求cosB、sinA
当a>0且x>0时,因为 ,所以
,所以 ,从而
,从而 (当x=
(当x= 时取等号).记函数
时取等号).记函数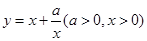 ,由上述结论可知:当x=
,由上述结论可知:当x= 时,该函数有最小值为2
时,该函数有最小值为2
(1)已知函数y1=x(x>0)与函数 ,则当x=时,y1+y2取得最小值为
,则当x=时,y1+y2取得最小值为
(2)已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>−1),求 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.