如图，菱形ABCD的边长为48cm，∠A=60°，动点P从点A出发，沿着线路AB—BD做匀速运动，动点Q从点D同时出发，沿着线路DC—CB—BA做匀速运动.
（1）求BD的长；
（2）已知动点P、Q运动的速度分别为8cm/s、10cm/s. 经过12秒后，P、Q分别到达M、N两点，若按角的大小进行分类，请问△AMN是哪一类三角形，并说明理由；
（3）设问题（2）中的动点P、Q分别从M、N同时沿原路返回，动点P的速度不变，动点Q的速度改变为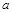
cm/s，经过3秒后，P、Q分别到达E、F两点，若△BEF与问题（2）中的△AMN相似，试求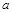的值.
如图，在以O为圆心的两个同心圆中，AB经过圆心O，且与小圆相交于点A．与大圆相交于点B．小圆的切线AC与大圆相交于点D，且CO平分∠ACB．
（1）试判断BC所在直线与小圆的位置关系，并说明理由；
（2）试判断线段AC，AD，BC之间的数量关系，并说明理由．
如图，将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置，D，D′分别是AB，A′B′的中点，且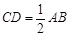
，已知AC=8cm，BC=6cm，求线段DD′的长．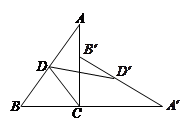
一个盒子里有完全相同的三个小球，球上分别标上数字﹣1、1、2．随机摸出一个小球（不放回）其数字记为p，再随机摸出另一个小球其数字记为q，求满足关于x的方程x2+px+q=0有实数根的概率．
如图，△ABC中，以AB为直径的⊙O交AC于点D，∠DBC=∠BAC．
（1）求证：BC是⊙O的切线．
（2）若⊙O的半径为2，∠BAC=30°，求图中阴影部分的面积．
某商店准备进一批季节性小家电，单价40元．经市场预测，销售定价为52元时，可售出180个，定价每增加1元，销售量净减少10个；定价每减少1元，销售量净增加10个．因受库存的影响，每批次进货个数不得超过180个，商店若将准备获利2000元，则应进货多少个？定价为多少元？