(本题12分)如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=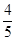 |PD|.
|PD|.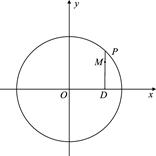
(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为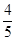 的直线被曲线C所截线段的长度.
的直线被曲线C所截线段的长度.
(本小题满分12分)已知向量 ,函数
,函数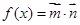 .
.
(1)求函数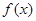 的单调递增区间;
的单调递增区间;
(2)在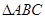 中,角
中,角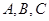 的对边分别为
的对边分别为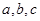 ,若
,若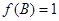 ,
,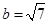 ,
,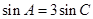 ,求
,求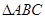 的面积.
的面积.
(本小题满分14分)已知 ,函数
,函数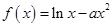 ,
, .(
.( 的图象连续不断)
的图象连续不断)
(Ⅰ) 求 的单调区间;
的单调区间;
(Ⅱ) 当 时,证明:存在
时,证明:存在 ,使
,使 ;
;
(Ⅲ) 若存在属于区间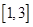 的
的 ,且
,且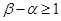 ,使
,使 ,证明:
,证明: .
.
(本小题满分14分)已知椭圆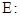
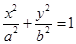 (
(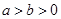 )的离心率为
)的离心率为 ,右焦点到直线
,右焦点到直线 的距离为
的距离为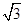 .
.
(1)求椭圆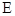 的方程;
的方程;
(2)已知点 ,斜率为
,斜率为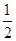 的直线
的直线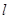 交椭圆
交椭圆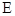 于两个不同点
于两个不同点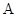 .
.  ,设直线
,设直线 与
与 的斜率分别为
的斜率分别为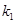 ,
,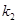 ,
,
①若直线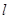 过椭圆
过椭圆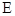 的左顶点,求此时
的左顶点,求此时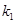 ,
,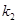 的值;
的值;
②试猜测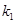 ,
,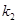 的关系,并给出你的证明.
的关系,并给出你的证明.
(本小题满分14分)如图,四棱锥 中,
中, ,底面
,底面 为梯形,
为梯形, ,
, ,且
,且 ,
, .
.
(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
(本小题满分14分)设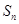 表示数列
表示数列 的前
的前 项和.
项和.
(1)若 为公比为
为公比为 的等比数列,写出并推导
的等比数列,写出并推导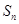 的计算公式;
的计算公式;
(2)若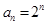 ,
, ,求证:
,求证: <1.
<1.