(本小题满分12分)
如图,直三棱柱ABC—A1B1C1中,AC=BC=1,∠ACB=90°,AA1= ,D是A1B1中点.
,D是A1B1中点.
(1)求证:C1D⊥AB1 ;
(2)当点F在BB1上什么位置时,会使得AB1⊥平面C1DF?并证明你的结论.
已知函数 (a为常数)是R上的奇函数,函数
(a为常数)是R上的奇函数,函数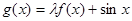
是区间[-1,1]上的减函数.
(1)求a的值;
(2)若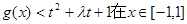 上恒成立,求t的取值范围
上恒成立,求t的取值范围
直四棱柱 中,底面
中,底面 为菱形,且
为菱形,且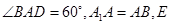 为
为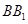 延长线上的一点,
延长线上的一点,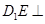 面
面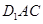 .
.
(Ⅰ)求二面角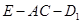 的大小;
的大小;
(Ⅱ)在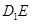 上是否存在一点
上是否存在一点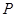 ,使
,使 面
面 ?若存在,求
?若存在,求 的值;不存在,说明理由.
的值;不存在,说明理由.
横峰中学将在四月份举行安全知识大奖赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题的正确率为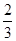 .
.
(Ⅰ)求选手甲可进入决赛的概率;
(Ⅱ)设选手甲在初赛中答题的个数为 ,试写出
,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望.
已知函数
.
(1)求函数
的最大值;
(2)求函数
的零点的集合
已知 ,等差数列{
,等差数列{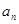 }中,
}中, ,
,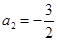 ,
,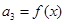 .求:⑴
.求:⑴ 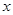 的值;⑵数列{
的值;⑵数列{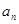 }的通项公式
}的通项公式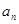 ;⑶
;⑶