如图,C为线段AB的中点,D在线段CB上,且AB=12,AD=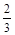 AB,求CD的长.
AB,求CD的长.
背景 :在图1中,已知线段AB,CD。其中点分别是E,F。
①若A(-1,0),B(3,0),则E点的坐标为________;
②若C(-2,2),D(-2,-1),则F点的坐标为_________;探究:在图2中,已知线段AB的端点坐标A(a,b),B(c,d),求出图中AB中点D的坐标(用含a,b,c,d的代数式表示),并给出求解过程;
归纳:无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(a,b),B(c,d),AB中点为D(x,y)时,x=______,y=_________(不必证明)。
运用:在图3中,一次函数y=x-2与反比例函数 的图像交点为A,B。
的图像交点为A,B。
①求出交点A,B的坐标;
②若以A、O、B、P为顶点的四边形是平行四边形,请利用上面的结论求出顶点P的坐标。
如图1,在△OAB中,∠OAB=90º,∠AOB=30º,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.求点B的坐标
求证:四边形ABCE是平行四边形;
如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.

如图19,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.求证:AC平分∠DAB
过点O作线段AC的垂线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作法);
若CD=4,AC=4,求垂线段OE的长.

在平面直角坐标系中,已知△ABC三个顶点的坐标分别为
画出△ABC,并求出AC所在直线的解析式。
画出△ABC绕点A顺时针旋转
 后得到的△A1B1C1,并求出△ABC在上述旋转过程中扫过的面积。
后得到的△A1B1C1,并求出△ABC在上述旋转过程中扫过的面积。
为更好地宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如右的调查问卷(单选).在随机调查了奉市全部5 000名司机中的部分司机后,统计整理并制作了如下的统计图:
根据以上信息解答下列问题:补全条形统计图,并计算扇形统计图中m=
该市支持选项B的司机大约有多少人?
若要从该市支持选项B的司机中随机选择100名,给他们发放“请勿酒驾”的提醒标志,则支持该选项的司机小李被选中的概率是多少?