(本小题14分)设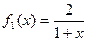 ,定义
,定义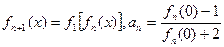 ,其中
,其中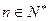 .
.
(1)求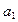 的值;
的值;
(2)求数列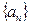 的通项公式;
的通项公式;
(3)若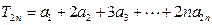 ,求
,求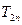 的值.
的值.
(本小题满分14分)
已知椭圆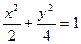 与射线y=
与射线y=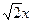 (x
(x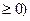 交于点A,过A作倾斜角互补的两条直线,
交于点A,过A作倾斜角互补的两条直线,
它们与椭圆的另一个交点分别为点B和点C.
(Ⅰ)求证:直线BC的斜率为定值,并求这个定值;
(Ⅱ)求三角形ABC的面积最大值.
(本小题满分14分)
已知函数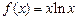 .
.
(Ⅰ)求 的最小值;
的最小值;
(Ⅱ)若对所有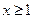 都有
都有 ,求实数
,求实数 的取值范围.
的取值范围.
本小题满分14分)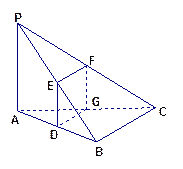
如图,已知三棱锥P—ABC中,PA⊥平面ABC,设AB、PB、PC的中点分别为D、E、F,
若过D、E、F的平面与AC交于点G.
(Ⅰ)求证点G是线段AC的中点;
(Ⅱ)判断四边形DEFG的形状,并加以证明;
(Ⅲ)若PA=8,AB=8,BC=6,AC=10,求几何体BC-DEFG的体积.
(本小题满分12分)
某市场搞国庆促销活动,一个人同时转动如图2所示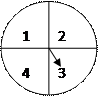
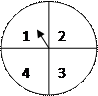 的两个转盘,记转盘(甲)得到的数
的两个转盘,记转盘(甲)得到的数 ,转盘(乙)
,转盘(乙)
得到的数为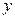 ,设
,设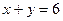 为中一等奖、
为中一等奖、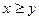
为中二等奖.
(Ⅰ)求中一等奖的概率;(甲)图2(乙)
(Ⅱ)求中二等奖的概率.