本小题满分14分)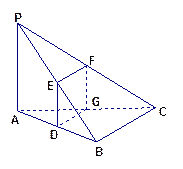
如图,已知三棱锥P—ABC中,PA⊥平面ABC,设AB、PB、PC的中点分别为D、E、F,
若过D、E、F的平面与AC交于点G.
(Ⅰ)求证点G是线段AC的中点;
(Ⅱ)判断四边形DEFG的形状,并加以证明;
(Ⅲ)若PA=8,AB=8,BC=6,AC=10,求几何体BC-DEFG的体积.
(文科)已知动直线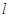 与椭圆
与椭圆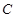 :
: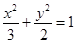 交于
交于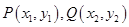 两不同点,且
两不同点,且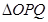 的面积
的面积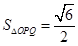 ,其中
,其中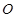 为坐标原点.
为坐标原点.
(Ⅰ)证明: 和
和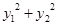 均为定值;
均为定值;
(Ⅱ)设线段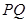 的中点为
的中点为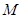 ,求
,求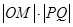 的最大值;
的最大值;
(Ⅲ)椭圆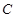 上是否存在三点
上是否存在三点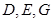 ,使得
,使得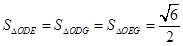 ?若存在,判断
?若存在,判断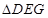 的形状;若不存在,请说明理由.
的形状;若不存在,请说明理由.
(理科)已知椭圆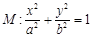 (
(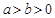 )的四个顶点恰好是一边长为
)的四个顶点恰好是一边长为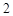 ,一内角为
,一内角为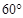 的菱形的四个顶点.
的菱形的四个顶点.
(1)求椭圆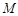 的方程;
的方程;
(2)直线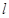 与椭圆
与椭圆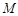 交于
交于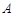 ,
,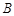 两点,且线段
两点,且线段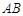 的垂直平分线经过点
的垂直平分线经过点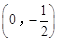 ,求
,求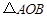 (
(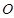 为原点)面积的最大值.
为原点)面积的最大值.
(文科)已知抛物线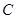 的顶点为原点,其焦点
的顶点为原点,其焦点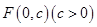 到直线
到直线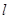 :
: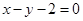 的距离为
的距离为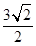 .设
.设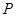 为直线
为直线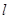 上的点,过点
上的点,过点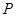 作抛物线
作抛物线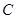 的两条切线
的两条切线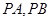 ,其中
,其中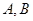 为切点.
为切点.
(Ⅰ)求抛物线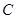 的方程;
的方程;
(Ⅱ)当点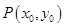 为直线
为直线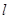 上的定点时,求直线
上的定点时,求直线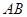 的方程;
的方程;
(Ⅲ)当点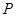 在直线
在直线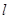 上移动时,求
上移动时,求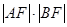 的最小值.
的最小值.
(理科)已知圆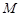 :
: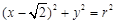 (
(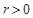 ).若椭圆
).若椭圆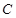 :
: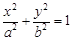 (
(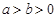 )的右顶点为圆
)的右顶点为圆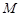 的圆心,离心率为
的圆心,离心率为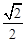 .(Ⅰ)求椭圆
.(Ⅰ)求椭圆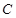 的方程;
的方程;
(Ⅱ)若存在直线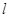 :
: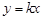 ,使得直线
,使得直线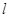 与椭圆
与椭圆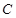 分别交于
分别交于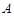 ,
,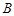 两点,与圆
两点,与圆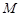 分别交于
分别交于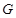 ,
,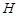 两点,点
两点,点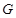 在线段
在线段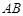 上,且
上,且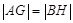 ,求圆
,求圆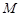 半径
半径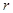 的取值范围.
的取值范围.
(文科)设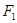 、
、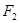 分别是椭圆
分别是椭圆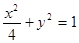 的左、右焦点.
的左、右焦点.
(Ⅰ)若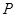 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求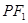 ·
·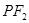 的最大值和最小值;
的最大值和最小值;
(Ⅱ)设过定点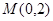 的直线
的直线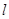 与椭圆交于不同的两点
与椭圆交于不同的两点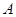 、
、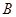 ,且∠
,且∠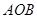 为锐角(其中
为锐角(其中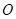 为坐标原点),求直线
为坐标原点),求直线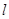 的斜率
的斜率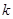 的取值范围.
的取值范围.