在直角坐标平面上有一点列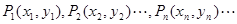 ,对一切正整数
,对一切正整数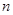 ,点
,点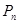 位于函数
位于函数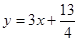 的图象上,且
的图象上,且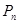 的横坐标构成以
的横坐标构成以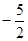 为首项,
为首项, 为公差的等差数列
为公差的等差数列 。
。
⑴求点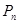 的坐标;
的坐标;
⑵设抛物线列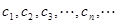 中的每一条的对称轴都垂直于
中的每一条的对称轴都垂直于 轴,第
轴,第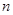 条抛物线
条抛物线 的顶点为
的顶点为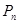 ,且过点
,且过点 ,记与抛物线
,记与抛物线 相切于
相切于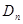 的直线的斜率为
的直线的斜率为 ,求:
,求: 。
。
⑶设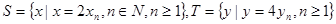 ,等差数列
,等差数列 的任一项
的任一项 ,其中
,其中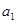 是
是 中的最大数,
中的最大数, ,求
,求 的通项公式。
的通项公式。
甲乙两个班级均为40人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为36人,乙班及格人数为24人.
(1)根据以上数据建立一个 的列联表;(2)试判断成绩与班级是否有关?
的列联表;(2)试判断成绩与班级是否有关?
参考公式: ;
;
| P(K2>k) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.84 |
5.024 |
6.635 |
7.879 |
10.83 |
已知函数 在
在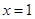 及
及 处取得极值.
处取得极值.
(1)求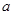 、
、 的值;(2)求
的值;(2)求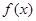 的单调区间.
的单调区间.
以直角坐标系的原点为极点,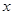 轴的正半轴为极轴建立极坐极系,并在两种坐极系中取相同的长度单位.已知直线的极坐标方程为
轴的正半轴为极轴建立极坐极系,并在两种坐极系中取相同的长度单位.已知直线的极坐标方程为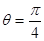 (
(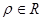 ),它与曲线
),它与曲线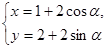 (
(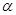 为参数)相交于两点A和B,求AB的长.
为参数)相交于两点A和B,求AB的长.
已知椭圆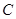 :
: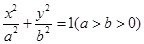 经过点
经过点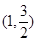 ,其离心率
,其离心率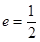 .
.
(1)求椭圆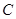 的方程;
的方程;
(2)过坐标原点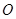 作不与坐标轴重合的直线
作不与坐标轴重合的直线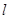 交椭圆
交椭圆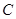 于
于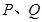 两点,过
两点,过 作
作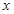 轴的垂线,垂足为
轴的垂线,垂足为 ,连接
,连接 并延长交椭圆
并延长交椭圆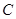 于点
于点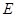 ,试判断随着
,试判断随着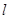 的转动,直线
的转动,直线 与
与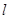 的斜率的乘积是否为定值?说明理由.
的斜率的乘积是否为定值?说明理由.
已知函数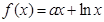 ,函数
,函数 的导函数
的导函数 ,且
,且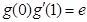 ,其中
,其中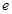 为自然对数的底数.
为自然对数的底数.
(1)求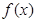 的极值;
的极值;
(2)若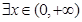 ,使得不等式
,使得不等式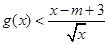 成立,试求实数
成立,试求实数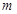 的取值范围;
的取值范围;