(本小题满分12分)
已知圆C: .
.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程;
(2)从圆C外一点P(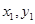 )向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
已知各项均为正数的等比数列 中,
中, .
.
(1)求公比 ;
;
(2)若 分别为等差数列
分别为等差数列 的第3项和第5项,求数列
的第3项和第5项,求数列 的通项公式.
的通项公式.
某电视台为宣传安徽,随机对安徽15~65岁的人群抽取了 人,回答问题“皖江城市带有哪几个城市?”统计结果如图表所示:
人,回答问题“皖江城市带有哪几个城市?”统计结果如图表所示:
| 组号 |
分组 |
回答正确的人数 |
回答正确的人数占本组的频率 |
| 第1组 |
[15,25) |
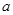 |
0.5 |
| 第2组 |
[25,35) |
18 |
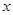 |
| 第3组 |
[35,45) |
 |
0.9[ |
| 第4组 |
[45,55) |
9 |
0.36 |
| 第5组 |
[55,65) |
3 |
 |
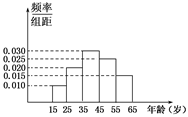
(1)分别求出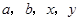 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
一个均匀的正四面体面上分别涂有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为 .
.
(1)记 ,求
,求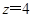 的概率;
的概率;
(2)若方程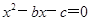 至少有一根
至少有一根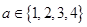 ,就称该方程为“漂亮方程”,求方程为“漂亮方程”的概率.
,就称该方程为“漂亮方程”,求方程为“漂亮方程”的概率.
为预防X病毒爆发,某生物技术公司研制出一种X病毒疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个样本分成三组,测试结果如下表:
| 分组 |
 组 组 |
 组 组 |
 组 组 |
| 疫苗有效 |
673 |
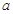 |
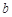 |
| 疫苗无效 |
77 |
90 |
 |
已知在全体样本中随机抽取1个,抽到 组疫苗有效的概率是0.33.
组疫苗有效的概率是0.33.
(1)现用分层抽样的方法在全体样本中抽取360个测试结果,应在 组抽取样本多少个?
组抽取样本多少个?
(2)已知 ,
, ,求通过测试的概率.
,求通过测试的概率.
已知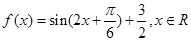 .
.
(1)求函数 的最小正周期和单调增区间.
的最小正周期和单调增区间.
(2)函数 的图象可以由函数
的图象可以由函数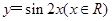 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?