(本小题满分10分)选修4-1几何证明选讲
如图,AB是 O的直径,BE为圆0的切线,点c为
O的直径,BE为圆0的切线,点c为 o 上不同于A、B的一点,AD为
o 上不同于A、B的一点,AD为 的平分线,且分别与BC 交于H,与
的平分线,且分别与BC 交于H,与 O交于D,与BE交于E,连结BD、CD.
O交于D,与BE交于E,连结BD、CD.
(I )求证:BD平分
(II)求证:AH•BH=AE•HC
已知△ 的面积
的面积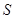 满足
满足 ,且
,且 ,
,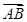 与
与 的夹角为
的夹角为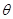 .
.
(1)求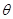 的取值范围;
的取值范围;
(2)求函数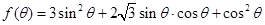 的最大值及最小值.
的最大值及最小值.
某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组: ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
(1)求直方图中 的值;
的值;
(2)求续驶里程在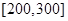 的车辆数;
的车辆数;
(3)若从续驶里程在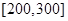 的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程为
的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程为 的概率.
的概率.
在△ 中,角
中,角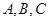 的对边分别为
的对边分别为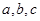 ,且满足
,且满足 .
.
(1)求角 的值;
的值;
(2)设 ,当
,当 取到最大值时,求角
取到最大值时,求角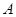 、角
、角 的值.
的值.
已知函数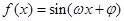 (
( ,
, )为偶函数,其图象上相邻的两个对称轴之间的距离为
)为偶函数,其图象上相邻的两个对称轴之间的距离为 .
.
(1)求 的解析式;
的解析式;
(2)若 ,求
,求 的值.
的值.
甲有大小相同的两张卡片,标有数字2、3;乙有大小相同的卡片四张,分别标有1、2、3、4.
(1)求乙随机抽取的两张卡片的数字之和为奇数的概率;
(2)甲、乙分别取出一张卡,比较数字,数字大者获胜,求乙获胜的概率.