长方体的全面积为11,十二条棱长度之和为24,求这个长方体的一条对角线长。
已知数列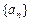 是公差为2的等差数列,其前
是公差为2的等差数列,其前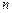 项和为
项和为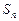 ,且
,且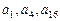 成等比数列.
成等比数列.
(1)求数列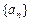 的通项公式;(2)求
的通项公式;(2)求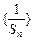 的前
的前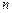 项和
项和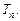
已知向量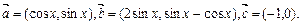
(1)若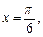 求向量
求向量 与
与 的夹角;
的夹角;
(2)当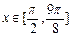 时,函数
时,函数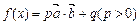 的最大值为1,最小值为
的最大值为1,最小值为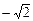 ,求
,求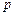 、
、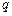 的值.
的值.
已知集合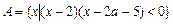 ,函数
,函数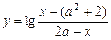 的定义域为集合
的定义域为集合
(1)若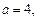 求集合
求集合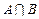 ;
;
(2)已知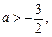 且
且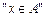 是
是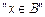 的必要条件,求实数
的必要条件,求实数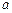 的取值范围.
的取值范围.
(本小题满分16分)如图, 、
、 是通过某城市开发区中心
是通过某城市开发区中心 的两条南北和东西走向的街道,连接
的两条南北和东西走向的街道,连接 、
、 两地之间的铁路线是圆心在
两地之间的铁路线是圆心在 上的一段圆弧.若点
上的一段圆弧.若点 在点
在点 正北方向,且
正北方向,且 ,点
,点 到
到 、
、 的距离分别为
的距离分别为 和
和 .
.
(1)建立适当坐标系,求铁路线所在圆弧的方程;
(2)若该城市的某中学拟在点 正东方向选址建分校,考虑环境问题,要求校址到点
正东方向选址建分校,考虑环境问题,要求校址到点 的距离大于
的距离大于 ,并且铁路线上任意一点到校址的距离不能少于
,并且铁路线上任意一点到校址的距离不能少于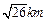 ,求该校址距点O的最近距离(注:校址视为一个点).
,求该校址距点O的最近距离(注:校址视为一个点).
(文科做)(本小题满分16分)
已知椭圆 过点
过点 ,离心率为
,离心率为 ,圆
,圆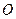 的圆心为坐标原点,直径为椭圆的短轴,圆
的圆心为坐标原点,直径为椭圆的短轴,圆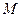 的方程为
的方程为 .过圆
.过圆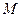 上任一点
上任一点 作圆
作圆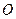 的切线
的切线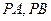 ,切点为
,切点为 .
.
(1)求椭圆的方程;
(2)若直线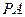 与圆
与圆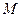 的另一交点为
的另一交点为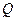 ,当弦
,当弦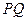 最大时,求直线
最大时,求直线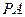 的直线方程;
的直线方程;
(3)求 的最值.
的最值.