(本小题满分12分)
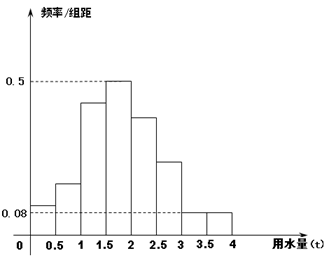
为了解某社区家庭的月均用水量(单位:吨),现从该社区随机抽查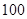 户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).
户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).
(Ⅰ)分别求出频率分布表中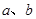 的值,并估计该社区家庭月均用水量不超过
的值,并估计该社区家庭月均用水量不超过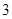 吨的频率;
吨的频率;
(Ⅱ)设 、
、 、
、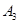 是户月均用水量为
是户月均用水量为 的居民代表,
的居民代表,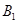 、
、 是户月均用水量为
是户月均用水量为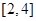 的居民代表. 现从这五位居民代表中任选两人参加水价论证会,请列举出所有不同的选法,并求居民代表
的居民代表. 现从这五位居民代表中任选两人参加水价论证会,请列举出所有不同的选法,并求居民代表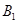 、
、 至少有一人被选中的概率.
至少有一人被选中的概率.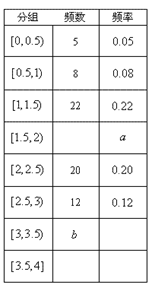
(本小题满分12分)
已知等比数列 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列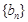 的前
的前 项和Sn.
项和Sn.
(本小题满分12分)在△ABC中,角A、B、C所对的边分别为a、b、c,且满足

(1)求△ABC的面积;
(2)若 的值.
的值.
(本小题满分7分) 选修4—5:不等式选讲
设函数 。
。
(Ⅰ)解不等式 ;
;
(Ⅱ)已知关于x的不等式 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
(本小题满分7分) 选修4—4:极坐标与参数方程
在极坐标系中,已知直线l的极坐标方程为 ,圆C的圆心是
,圆C的圆心是 ,半径为
,半径为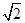 。
。
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)求直线l被圆C所截得的弦长
(本小题满分7分)选修4-2:矩阵与变换
二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).
(Ⅰ)求矩阵M;
(Ⅱ)设直线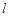 在变换M作用下得到了直线m:2x-y=4,求
在变换M作用下得到了直线m:2x-y=4,求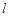 的方程
的方程