为了保护环境，发展低碳经济，某单位在国家科研部门的支持下，采用了新工艺，把二氧化碳转化为一种可利用的化工产品．已知该单位每月的处理量最少为400吨，最多为600吨，月处理成本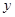
（元）与月处理量
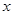（吨）之间的函数关系可近似的表示为：
，且每处理一吨二氧化碳得到可利用的化工产品价值为100元．
（1）该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低？
（2）该单位每月能否获利？如果获利，求出最大利润；如果不获利，则国家至少需要补贴多少元才能使该单位不亏损？
多哈亚运会中，中国女排与日本女排以“五局三胜”制进行决赛，根据以往战况，中国女排每一局赢的概率为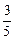
。已知比赛中，第一局日本女排先胜一局，在这个条件下，（Ⅰ）求中国女排取胜的概率
（Ⅱ）设决赛中比赛总的局数
，求的分布列及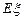
（（Ⅰ）（Ⅱ）均用分数作答）
在一个盒子中，放有标号分别为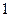
，
，
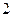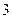的三张卡片，现从这个盒子中，有放回地先后抽得两张卡片的标号分别为
、
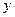，记
．
（Ⅰ）求随机变量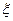
的最大值，并求事件“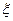取得最大值”的概率；
（Ⅱ）求随机变量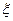的分布列和数学期望．
甲、乙两支足球队，苦战120分钟，比分为1 ：1，现决定各派5名队员，每人射一个点球决定胜负，假设两支球队派出的队员点球命中率均为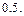
⑴两队球员一个间隔一个出场射球，有多少种不同的出场顺序？
⑵甲、乙两队各射完5个点球后，再次出现平局的概率是多少？
某同学上楼梯的习惯每步走1阶或2阶，现有一个11阶的楼梯 ，该同学从第1阶到第11阶用7步走完。
(1)求该同学恰好有连着三步都走2阶的概率；
(2)记该同学连走2阶的最多步数为ζ，求随机事件ζ的分布列及其期望。
某售货员负责在甲、乙、丙三个柜面上售货．如果在某一小时内各柜面不需要售货员照顾的概率分别为0.9,0.8，0.7．假定各个柜面是否需要照顾相互之间没有影响，求在这个小时内：
（1）只有丙柜面需要售货员照顾的概率；
（2）三个柜面最多有一个需要售货员照顾的概率；
（3）三个柜面至少有一个需要售货员照顾的概率．