(本小题满分12分)
设双曲线 的方程为
的方程为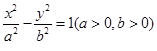 ,
, 、
、 为其左、右两个顶点,
为其左、右两个顶点, 是双曲线
是双曲线 上的任意一点,作
上的任意一点,作 ,
,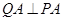 ,垂足分别为
,垂足分别为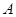 、
、 ,
, 与
与 交于点
交于点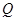 .
.
(1)求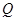 点的轨迹
点的轨迹 方程;
方程;
(2)设 、
、 的离心率分别为
的离心率分别为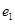 、
、 ,当
,当 时,求
时,求 的取值范围.
的取值范围.
设X为随机变量,从棱长为a的正方体 ,的八个顶点中任取四个点,当四点共面时,X=0;当四点不共面时,X的值为四点组成的四面体的体积.
,的八个顶点中任取四个点,当四点共面时,X=0;当四点不共面时,X的值为四点组成的四面体的体积.
(1)求概率P(X=0);
(2)求X的分布列,并求其数学期望E(X).
在 ABC中,记角A,B,C的对边为a,b,c,角A为锐角,设向量
ABC中,记角A,B,C的对边为a,b,c,角A为锐角,设向量
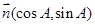 ,且
,且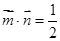 .
.
(1)求角A的大小及向量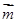 与
与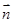 的夹角;
的夹角;
(2)若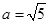 ,求
,求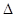 ABC面积的最大值.
ABC面积的最大值.
(本题满分 分)已知
分)已知 ,函数
,函数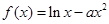 .(
.( 的图像连续不断)
的图像连续不断)
(1)求 的单调区间;
的单调区间;
(2)当 时,证明:存在
时,证明:存在 ,使
,使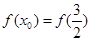 ;
;
(3)若存在均属于区间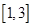 的
的 ,且
,且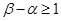 ,使
,使 ,证明
,证明
如图,已知椭圆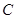 :
: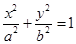 ,其左右焦点为
,其左右焦点为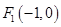 及
及 ,过点
,过点 的直线交椭圆
的直线交椭圆 于
于 两点,线段
两点,线段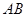 的中点为
的中点为 ,
,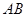 的中垂线与
的中垂线与 轴和
轴和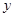 轴分别交于
轴分别交于 两点,且
两点,且 、
、 、
、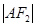 构成等差数列.
构成等差数列.
(1)求椭圆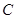 的方程;
的方程;
(2)记△ 的面积为
的面积为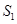 ,△
,△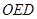 (
(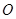 为原点)的面积为
为原点)的面积为 .试问:是否存在直线
.试问:是否存在直线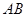 ,使得
,使得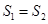 ?说明理由.
?说明理由.
(本题满分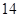 分)设数列
分)设数列 的前
的前 项和为
项和为 ,已知
,已知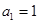 ,
, ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)证明:对一切正整数 ,有
,有 .
.