对某校高二年级学生参加社会实践活动次数进行统计，随机抽取M名-优题课

题文

对某校高二年级学生参加社会实践活动次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社会实践活动的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：

分组	频数	频率
	10	0.25
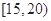	26	n
	m	P
	1	0.025
合计	M	1

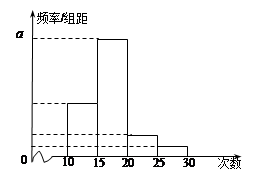
（Ⅰ）求出表中M，P及图中的值；
（Ⅱ）在所取样本中，从参加社会实践活动的次数不少于20次的学生中任选2人，求恰有一人参加社会实践活动次数在区间内的概率．

科目数学题型解答题难度较易

知识点：误差估计

登录免费查看答案和解析

相关试题

已知函数 $f (x) = \cos x \cdot \sin (x + \frac{π}{3}) - \sqrt{3} \cos^{2} x + \frac{\sqrt{3}}{4}$ ， $x \in R$ ．
（1）求 $f (x)$ 的最小正周期；
（2）求 $f (x)$ 在闭区间 $[- \frac{π}{4}, \frac{π}{4}]$ 上的最大值和最小值．

设函数 $f (x) = |x + \frac{1}{a}| + |x - a| (a > 0)$ .

（1）证明： $f (x) \geq 2$ ；
（2）若 $f (3) < 5$ ，求 $a$ 的取值范围.

在直角坐标系 $x o y$ 中，以坐标原点为极点， $x$ 轴为极轴建立极坐标系，半圆 $C$ 的极坐标方程为 $ρ = 2 \cos θ$ ， $θ \in [0, \frac{π}{2}]$ .
（1）求 $C$ 的参数方程；

（2）设点 $D$ 在 $C$ 上， $C$ 在 $D$ 处的切线与直线 $l : y = \sqrt{3} x + 2$ 垂直，根据（1）中你得到的参数方程，确定 $D$ 的坐标.

如图， $P$ 是 $O$ 外一点， $P A$ 是切线， $A$ 为切点，割线 $P B C$ 与 $O$ 相交于点 $B, C$ ， $P C = 2 P A$ ， $D$ 为 $P C$ 的中点， $A D$ 的延长线交 $O$ 于点 $E$ .

证明：（1） $B E = E C$ ；
（2） $A D \cdot D E = 2 P B^{2}$

已知函数 $f (x) = e^{x} - e^{- x} - 2 x$ .
（1）讨论 $f (x)$ 的单调性；
（2）设 $g (x) = f (2 x) - 4 b f (x)$ ，当 $x > 0$ 时， $g (x) > 0$ ,求 $b$ 的最大值；
（3）已知 $1.4142 < \sqrt{2} < 1.4143$ ，估计 $\ln 2$ 的近似值（精确到0.001）.

试卷网试题网古诗词网作文网范文网