(本小题满分12分)
如图,四棱锥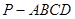 中,底面
中,底面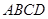 是边长为2的正方形,
是边长为2的正方形, ,且
,且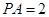 ,
,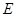 为
为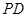 中点.
中点.
(1)求证: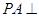 平面
平面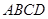 ;
;
(2)求二面角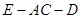 的余弦值.
的余弦值.
某工厂对某种产品的产量与成本的资料分析后有如下数据:
| 产量x(千件) |
2 |
3 |
5 |
6 |
| 成本y(万元) |
7 |
8 |
9 |
12 |
经过分析,知道产量x和成本y之间具有线性相关关系.
(Ⅰ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程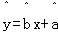 ;
;
(Ⅱ)试根据(1)求出的线性回归方程,预测产量为10千件时的成本.
已知函数 ,
, 是都不为零的常数.
是都不为零的常数.
(1)若函数 在
在 上是单调函数,求
上是单调函数,求 满足的条件;
满足的条件;
(2)设函数 ,若
,若 有两个极值点
有两个极值点 ,求实数
,求实数 的取值范围.
的取值范围.
已知椭圆C: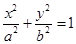 的焦距为4,且与椭圆
的焦距为4,且与椭圆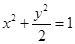 有相同的离心率,斜率为
有相同的离心率,斜率为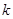 的直线
的直线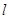 经过点M(0,1),与椭圆C交于不同的两点A ,B.
经过点M(0,1),与椭圆C交于不同的两点A ,B.
(1)求椭圆C的标准方程;
(2)当椭圆C的右焦点F在以AB为直径的圆内时,求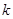 的取值范围.
的取值范围.
已知函数
 .
.
(1)求函数 的极值;
的极值;
(2)当 时,求
时,求 的最值.
的最值.
已知抛物线 的焦点为
的焦点为 ,抛物线上的点
,抛物线上的点 到准线的距离为
到准线的距离为 .
.
(1)求抛物线的标准方程;
(2)设直线 与抛物线的另一交点为
与抛物线的另一交点为 ,求
,求 的值.
的值.