已知数列 的前
的前 项和为
项和为 ,
,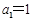 ,
,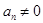 ,
,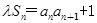 ,其中
,其中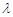 为常数.
为常数.
(1)证明:数列 是等差数列;
是等差数列;
(2)是否存在实数λ,使得 为等差数列?并说明理由;
为等差数列?并说明理由;
(3)若 为等差数列,令
为等差数列,令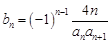 ,求数列
,求数列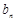 的前
的前 项和
项和 .
.
已知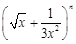 的第五项的二项式系数与第三项的二项式系数的比是
的第五项的二项式系数与第三项的二项式系数的比是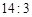 ,
,
(1)求n;
(2)求展开式中常数项.
从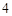 名男同学中选出
名男同学中选出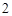 人,
人, 名女同学中选出
名女同学中选出 人,并将选出的
人,并将选出的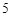 人排成一排.
人排成一排.
(1)共有多少种不同的排法?
(2)若选出的5人排队,男、女同学各排一排,共有多少种不同的排法?(用数字表示)
某校200位学生期末考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是: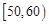 、
、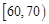 、
、 、
、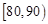 、
、 .
.
(1)求图中 的值;
的值;
(2)根据频率分布直方图,估计这200名学生物理成绩的平均值和中位数.
已知圆x2+y2+2ax-2ay+2a2-4a=0(0<a≤4)的圆心为C,直线l:y=x+m.
(1)若m=4,求直线l被圆C所截得弦长的最大值;
(2)若直线l是圆心下方的切线,当a在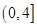 的变化时,求m的取值范围.
的变化时,求m的取值范围.
已知圆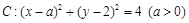 及直线
及直线 .当直线
.当直线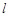 被圆
被圆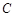 截得的弦长为
截得的弦长为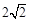 时,
时,
求(1)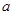 的值;
的值;
(2)求过点 并与圆
并与圆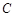 相切的切线方程.
相切的切线方程.