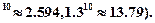若函数 在区间(0,1)、(1,2)内各有一个零点,求
在区间(0,1)、(1,2)内各有一个零点,求 的取值范围.
的取值范围.
甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为 ,且各局胜负相互独立.求:
(Ⅰ)打满3局比赛还未停止的概率;
(Ⅱ)比赛停止时已打局数 的分别列与期望 。
设
的内角
的对边分别为
且
.求:
(Ⅰ)
的值;
(Ⅱ) 的值.
备选题:已知函数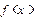 是定义在
是定义在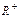 上的减函数,并且满足
上的减函数,并且满足 ,
,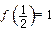 .
.
①求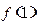 的值;
的值;
②解不等式: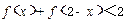 .
.
已知f(x)是定义在[-1,1]上的奇函数. 当a, b∈[-1,1],且a+b≠0时,有
(1)判断函数f(x)的的单调性,并给以证明;
(2)若f(1)=1,且f(x)≤m2-2bm+1对所有x∈[-1,1],b∈[-1,1]恒成立,求实数m的取值范围.
某企业进行技术改造,有两种方案可供选择:甲方案--- 一次性贷款10万元,第一年可获利1万元,以后每年比前一年增加30%的利润 ;乙方案---每年贷款1万元,第一年可获利1万元,以后每年却比前一年增加利润5千元,两种方案使用期都是10年,到期一次性还本付息,若银行贷款利息均按年息10%的复利计算 ,试比较两种方案的优劣(计算时精确到千元,并取1.1