如图,在四棱锥P-ABCD中,底面为直角梯形ABCD,AD∥BC,∠BAD=90O,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.(1)求证:PB⊥DM;(2)求CD与平面ADMN所成角的正弦值;(3)在棱PD上是否存在点E,且PE∶ED=λ,使得二面角C-AN-E的平面角为60o.若存在求出λ值，若不存在，请说明理由。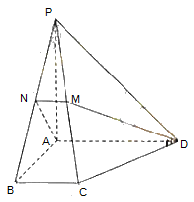
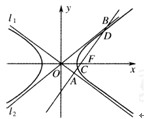
如图，双曲线的中心在坐标原点O，焦点在x轴上，两条渐近线分别为l1，l2，经过右焦点F垂直于l1的直线分别交l1，l2于A，B两点．又已知该双曲线的离心率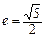
．
（1）求证：
，
，
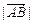依次成等差数列；
（2）若F(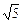
，0)，求直线AB在双曲线上所截得的弦CD的长度．
已知函数f(x)＝x3＋3ax－1的导函数f ′ (x)，g(x)＝f ′(x)－ax－3．
（1）当a＝－2时，求函数f(x)的单调区间；
（2）若对满足－1≤a≤1的一切a的值，都有g(x)＜0，求实数x的取值范围；
（3）若x·g ′(x)＋lnx＞0对一切x≥2恒成立，求实数a的取值范围．
如图，四棱锥P-ABCD的底面为矩形，侧棱PD垂直于底面，PD＝DC＝2BC，E为棱PC上的点，且平面BDE⊥平面PBC．
（1）求证：E为PC的中点；
（2）求二面角A-BD-E的大小．
某工厂2010年第三季度生产的A，B，C，D四种型号的产品产量用条形图形表示如图，现用分层抽样的方法从中选取50件样品参加2011年4月份的一个展销会。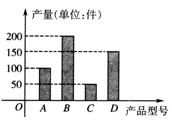
（1）A，B，C，D型号的产品各抽取多少件？
（2）从50件样品随机地抽取2件，求这2件产品恰好是不同型号产品的概率。
（3）从A，C型号的样品中随机地抽取3件，用ξ表示抽取A型号的产品件数，求ξ的分布列和数学期望
已知△ABC的周长为6，角A，B，C所对的边a，b，c成等比数列
（1）求角B及边b的最大值；
（2）设△ABC的面积为S，求S＋
最大值