如图,四棱锥P-ABCD的底面为矩形,侧棱PD垂直于底面,PD=DC=2BC,E为棱PC上的点,且平面BDE⊥平面PBC.
(1)求证:E为PC的中点;
(2)求二面角A-BD-E的大小.
已知a,b,c分别是△ABC的三个内角A、B、C的对边.
(Ⅰ)若△ABC面积为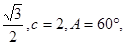 求a,b的值;
求a,b的值;
(Ⅱ)若acosA=bcosB,试判断△ABC的形状.
已知数列{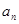 }满足
}满足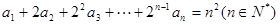
⑴求数列{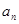 }的通项公式;⑵求数列{
}的通项公式;⑵求数列{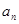 }的前
}的前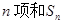 .
.
(本小题满分14分)
已知关于x的函数 ,其导函数
,其导函数 .
.
(1)如果函数 试确定b、c的值;
试确定b、c的值;
(2)设当 时,函数
时,函数 的图象上任一点P处的切线斜率为k,若
的图象上任一点P处的切线斜率为k,若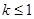 ,求实数b的取值范围。
,求实数b的取值范围。
(本小题满分12分)热力公司为某生活小区铺设暖气管道,为减 少热量损耗,管道外表需要覆盖保温层。经测算要覆盖可使用20年的保温层,每厘米厚的保温层材料成本为2万元,小区每年的气量损耗用
少热量损耗,管道外表需要覆盖保温层。经测算要覆盖可使用20年的保温层,每厘米厚的保温层材料成本为2万元,小区每年的气量损耗用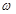 (单位:万元)与保温层厚度
(单位:万元)与保温层厚度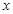 (单位:
(单位: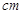 )满足关系:
)满足关系: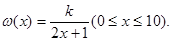 若不加保温层,每年热量损耗费用为5万元。设保温费用与20年的热量损耗费用之和为
若不加保温层,每年热量损耗费用为5万元。设保温费用与20年的热量损耗费用之和为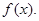
(1)求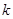 的值及
的值及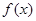 的表达式;
的表达式;
(2)问保温层多厚时,总费用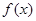 最小,并求最小值。
最小,并求最小值。
(本小题满分12分)设 是公比大于1的等比数列,
是公比大于1的等比数列, 为数列
为数列 的前
的前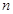 项和,已知
项和,已知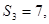 且
且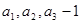 成等差数列。
成等差数列。
(1)求数列 的通项公式;
的通项公式;
(2)若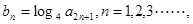 求和:
求和: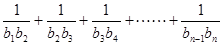 。
。