如图，椭圆长轴端点为
，
为椭圆中心，
为椭圆的右焦点，
且
,
.
（1）求椭圆的标准方程；
（2）记椭圆的上顶点为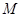
，直线
交椭圆于
两点，问：是否存在直线，使点恰为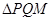
的垂心？若存在，求出直线的方程;若不存在，请说明理由.
已知数列{an}满足a1＝3，an＋1＝an＋p·3n(n∈N*，p为常数)，a1，a2＋6，a3成等差数列．
(1)求p的值及数列{an}的通项公式；
(2)设数列{bn}满足bn＝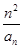
，证明：bn≤
.
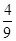一个袋子装有大小形状完全相同的9个球，其中5个红球编号分别为1,2,3,4,5,4个白球编号分别为1,2,3,4，从袋中任意取出3个球．
(1)求取出的3个球编号都不相同的概率；
(2)记X为取出的3个球中编号的最小值，求X的分布列与数学期望．
已知函数f(x)＝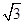
sin xcos x＋cos 2x－
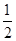，△ABC三个内角A，B，C的对边分别为a，b，c，且f(B)＝1.
(1)求角B的大小；
(2)若a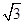＝，b＝1，求c的值．
已知函数f(x)＝ex－kx2，x∈R.
(1)若k＝
，求证：当x∈(0，＋∞)时，f(x)>1；
(2)若f(x)在区间(0，＋∞)上单调递增，试求k的取值范围；
(3)求证：
<e4(n∈N*)．．
设椭圆C：
＝1(a>b>0)的离心率e＝
，右焦点到直线
＝1的距离d＝
，O为坐标原点．
(1)求椭圆C的方程；
(2)过点O作两条互相垂直的射线，与椭圆C分别交于A，B两点，证明，点O到直线AB的距离为定值，并求弦AB长度的最小值．