已知函数 ,且
,且
(1)求 ;
;
(2)判断 的奇偶性;
的奇偶性;
(3)试判断 在
在 上的单调性,并证明。
上的单调性,并证明。
(本小题满分12分)已知集合 ,
, .
.
(1)在区间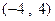 上任取一个实数
上任取一个实数 ,求“
,求“ ”的概率;
”的概率;
(2)设 为有序实数对,其中
为有序实数对,其中 是从集合
是从集合 中任取的一个整数,
中任取的一个整数, 是从集合
是从集合 中任取的一个整数,求“
中任取的一个整数,求“ ”的概率.
”的概率.
(本小题满分12分)
在△ABC中,内角A,B,C所对边长分别为 ,
, ,
, ,
, .
.
(Ⅰ)求 的最大值及
的最大值及 的取值范围;
的取值范围;
(Ⅱ)求函数 的最值.
的最值.
(本小题满分12分)
设函数 曲线y=f(x)通过点(0,2a+3),且
曲线y=f(x)通过点(0,2a+3),且
在点(-1,f(-1))处的切线垂直于y轴.
(Ⅰ)用a分别表示b和c;
(Ⅱ)当bc取得最小值时,求函数g(x)=-f(x)e-x的单调区间.
(本小题满分10分)
已知曲线y=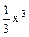 在x=x0处的切线L经过点P(2,
在x=x0处的切线L经过点P(2, ),求切线L的方程。
),求切线L的方程。
(本小题满分12分)
已知双曲线过点P ,它的
,它的 渐近线方程为
渐近线方程为
(1)求双曲线的标准方程;
(2)设F1和F2是这双曲线的左、右焦点,点P在这双曲线上,且|PF1|·|PF2|=32,求∠F1PF2的大小.