(本小题满分12分)
设圆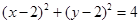 的切线
的切线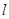 与两坐标轴交于点
与两坐标轴交于点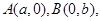
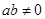 .
.
(1)证明: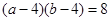 ;
;
(2)若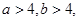 求△AOB的面积的最小值.
求△AOB的面积的最小值.
(本小题满分12分)
一个四棱锥P-ABCD的正视图是边长为2的正方形及其一条对角线,侧视图和俯视图全全等的等腰直角三角形,直角边长为2,直观图如图.
(1)求四棱锥P-ABCD的体积:
(2)求直线PC和面PAB所成线面角的余弦值;
(3)M为棱PB上的一点,当PM长为何值时,CM⊥PA?
已知数列 ,设
,设 ,数列
,数列 。
。
(1)求证: 是等差数列; (2)求数列
是等差数列; (2)求数列 的前n项和Sn.
的前n项和Sn.
.(本小题满分12分)
设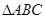 的内角
的内角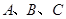 的对边分别为
的对边分别为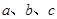 ,且
,且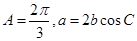 ,求:
,求:
(1)角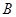 的值;
的值;
(2)函数 在区间
在区间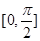 上的最大值及对应的x值.
上的最大值及对应的x值.
(本小题满分14分)已知椭圆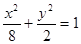 经过点M(2,1),O为坐标原点,平行于OM的直线l在y轴上的截距为m(m≠0)
经过点M(2,1),O为坐标原点,平行于OM的直线l在y轴上的截距为m(m≠0)
(1)当 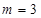 时,判断直线l与椭圆的位置关系;
时,判断直线l与椭圆的位置关系;
(2)当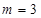 时,P为椭圆上的动点,求点P到直线l距离的最小值;
时,P为椭圆上的动点,求点P到直线l距离的最小值;
(3)如图,当l交椭圆于A、B两个不同点时,求证:
直线MA、MB与x轴始终围成一个等腰三角形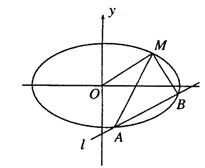
(本小题满分12分)
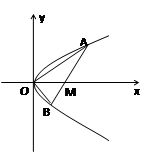
如图,已知直线 与抛物线
与抛物线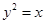 相交于
相交于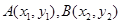 两点,
两点,
与 轴相交于点
轴相交于点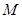 ,若
,若 .
.
(1)求证: 点的坐标为(1,0);
点的坐标为(1,0);
(2)求△AOB的面积的最小值.