(本题满分10分)
若直线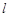 过点(0,3)且与抛物线y2=2x只有一个公共点,求该直线方程.
过点(0,3)且与抛物线y2=2x只有一个公共点,求该直线方程.
(本小题12分)如图,四棱锥P-ABCD是底面边长为1的正方形,PD ⊥BC,PD=1,PC= .
.
(Ⅰ)求证:PD⊥面ABCD;
(Ⅱ)求二面角A-PB-D的大小.
(本小题12分)已知函数 的图象与x、y轴分别相交于点A、 B,
的图象与x、y轴分别相交于点A、 B, (
( 、
、 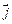 分别是与x、y轴正半轴同方向的单位向量), 函数
分别是与x、y轴正半轴同方向的单位向量), 函数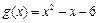
(1) 求k、b的值;
(2) 当x满足 时,求函数
时,求函数 的最小值
的最小值
(本小题12分)已知函数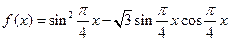
(1)求 的最大值及此时
的最大值及此时 的值
的值
(2)求 的值.
的值.
(本小题满分12分)
已知函数f(x)=4x3-3x2sin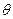 +
+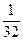 的极小值大于零,其中x∈R,
的极小值大于零,其中x∈R, 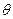 ∈[0,
∈[0,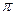 ].
].
(1).求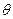 的取值范围.
的取值范围.
(2).若在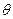 的取值范围内的任意
的取值范围内的任意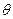 ,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.
,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.
(3).设x0> ,f(x0) >
,f(x0) > ,若f[f(x0)]=x0,求证f(x0)=x0
,若f[f(x0)]=x0,求证f(x0)=x0
(本小题满分12分)
已知定点A(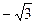 ,0),B是圆C:(x-
,0),B是圆C:(x- )2+y2=16,(C为圆心)上的动点,AB的垂直平分线与BC交与点E.
)2+y2=16,(C为圆心)上的动点,AB的垂直平分线与BC交与点E.
(1)求动点E的轨迹方程.
(2)设直线l:y="kx+m" (k≠0,m>0)与E的轨迹交与P,Q两点,且以PQ为对角线的菱形的一顶点为M(-1,0),求△OPQ面积的最大值及此时直线l的方程.