.(满分12分)已知: ,当
,当 时,
时,  ;
; 时,
时,
(1)求 的解析式
的解析式
(2)c为何值时, 的解集为R.
的解集为R.
已知函数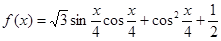
(Ⅰ)求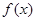 的单调递增区间;
的单调递增区间;
(Ⅱ)在锐角△ABC中,角A、B、C的对边分别是 、b、c满足
、b、c满足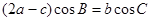 ,求
,求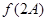 的取值范围.
的取值范围.
给定函数
(1)a=-4时,求函数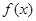 的单调区间;
的单调区间;
(2)当 时,求函数
时,求函数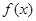 的极值点.
的极值点.
已知动点P与双曲线 的两个焦点F1,F2的距离之和为4.
的两个焦点F1,F2的距离之和为4.
(1)求动点P的轨迹C的方程;
(2)若M为曲线C上的动点,以M为圆心,MF2为半径做圆M.若圆M与y轴有两个交点,求点M横坐标的取值范围.
某地兴建一休闲商业广场,欲在如图所示的一块不规则用地规划建成一个矩形的商业楼区,余下作为休闲区域,已知 ,且AB=BC=2AO=4km,曲线段OC是以O为顶点且开口向上的抛物线的一段,如果要使矩形的相邻两边分别落在AB、BC上,且一个顶点落在曲线段OC上,应如何规划才能使矩形商业楼区的用地面积最大?
,且AB=BC=2AO=4km,曲线段OC是以O为顶点且开口向上的抛物线的一段,如果要使矩形的相邻两边分别落在AB、BC上,且一个顶点落在曲线段OC上,应如何规划才能使矩形商业楼区的用地面积最大?
已知数列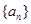 的前n项和为
的前n项和为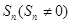 ,且
,且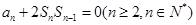 ,
,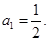
(1)求证: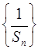 是等差数列;
是等差数列;
(2)求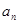 ;
;
(3)若