设函数 ,其中,角
,其中,角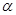 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与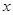 轴非负半轴重合,终边经过点
轴非负半轴重合,终边经过点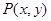 ,且
,且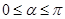 .
.
(1)若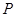 点的坐标为(-
点的坐标为(-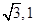 ),求
),求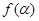 的值;
的值;
(2)若点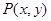 为平面区域
为平面区域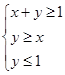 上的一个动点,试确定角
上的一个动点,试确定角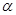 的取值范围,并求函数
的取值范围,并求函数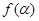 的值域.
的值域.
设命题p:函数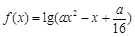 的定义域为R;命题q:
的定义域为R;命题q: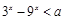 对一切的实数
对一切的实数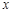 恒成立,如果命题“p且q”为假命题,求实数a的取值范围.
恒成立,如果命题“p且q”为假命题,求实数a的取值范围.
设函数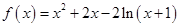 .
.
(1)求函数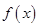 的单调区间;
的单调区间;
(2)当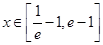 时,是否存在整数
时,是否存在整数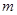 ,使不等式
,使不等式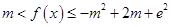 恒成立?若存在,求整数
恒成立?若存在,求整数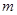 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)关于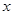 的方程
的方程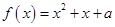 在
在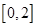 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数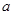 的取值范围.
的取值范围.
某工厂有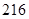 名工人,现接受了生产
名工人,现接受了生产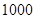 台
台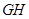 型高科技产品的总任务.已知每台
型高科技产品的总任务.已知每台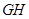 型产品由
型产品由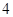 个
个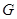 型装置和
型装置和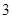 个
个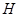 型装置配套组成,每个工人每小时能加工
型装置配套组成,每个工人每小时能加工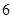 个
个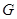 型装置或
型装置或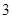 个
个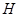 型装置.现将工人分成两组同时开始加工,每组分别加工一种装置(完成自己的任务后不再支援另一组).设加工
型装置.现将工人分成两组同时开始加工,每组分别加工一种装置(完成自己的任务后不再支援另一组).设加工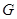 型装置的工人有
型装置的工人有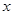 人,他们加工完
人,他们加工完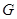 型装置所需时间为
型装置所需时间为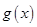 ,其余工人加工完
,其余工人加工完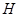 型装置所需时间为
型装置所需时间为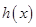 (单位:小时,可不为整数).
(单位:小时,可不为整数).
(1)写出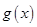 、
、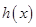 的解析式;
的解析式;
(2)写出这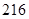 名工人完成总任务的时间
名工人完成总任务的时间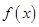 的解析式;
的解析式;
(3)应怎样分组,才能使完成总任务用的时间最少?
已知向量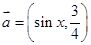 ,
,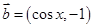 .
.
(1)当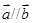 时,求
时,求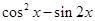 的值;
的值;
(2)设函数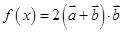 ,已知在
,已知在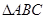 中,内角
中,内角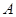 、
、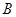 、
、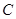 的对边分别为
的对边分别为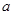 、
、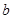 、
、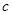 ,若
,若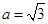 ,
,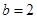 ,
,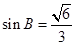 ,求
,求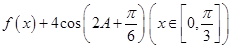 的取值范围.
的取值范围.