(本小题满分13分)
设a、b、c分别是先后掷一枚质地均匀的正方体骰子三次得到的点数.
(1)求使函数 在R上不存在极值点的概率;
在R上不存在极值点的概率;
(2)设随机变量 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
已知函数 。
。
(1)当a=-1时,求函数f(x)的最大值、最小值及单调区间;
(2)求实数a的取值范围,使y=f(x)在区间[-5,5]上是单调函数。
如图,正方体ABCD-A1B1C1D1的棱长为2。
(1)求异面直线BC1与B1D1所成的角;
(2)求三棱锥A1-AB1D1的体积。
计算:(1)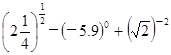 ;
;
(2)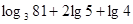
如图,是一个几何体的三视图,正视图和侧视图都是由一个边长为2的等边三角形和一个长为2宽为1的矩形组成。
(1)求此几何体的表面积;
(2)求此几何体的体积。
已知双曲线C与椭圆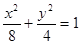 有相同的焦点,实半轴长为
有相同的焦点,实半轴长为 .
.
(Ⅰ)求双曲线 的方程;
的方程;
(Ⅱ)若直线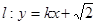 与双曲线
与双曲线 有两个不同的交点
有两个不同的交点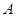 和
和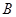 ,且
,且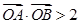 (其中
(其中 为原点),求
为原点),求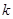 的取值范围.
的取值范围.