设双曲线方程为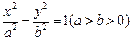
，P为双曲线上任意一点，F为双曲线的一个焦点，讨论以|PF|为直径的圆与圆x2＋y2=a2的位置关系．
设F1、F2为曲线C1∶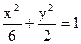
的焦点，P是曲线C2∶
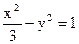与C1的一个交点，求的值．
垂直于x轴的直线交双曲线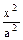
－
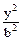=1右支于M，N两点，A1，A2为双曲线的左右两个顶点，求直线A1M与A2N的交点P的轨迹方程，并指出轨迹的形状．
双曲线中心在原点，坐标轴为对称轴，与圆x2＋y2=17交于A（4，－1）．若圆在点A的切线与双曲线的一条渐近线平行，求双曲线的方程．
设F1(-c，0)、F2(c，0)是椭圆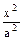
+
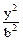=1(a>b>0)的两个焦点，P是以F1F2为直径的圆与椭圆的一个交点，若∠PF1F2=5∠PF2F1，求椭圆的离心率
