(本小题满分12分)
已知函数
(1)若函数 在
在 上为增函数,求正实数
上为增函数,求正实数 的取值范围;
的取值范围;
(2)当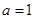 时,求
时,求 在
在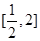 上的最大值和最小值;
上的最大值和最小值;
(3) 当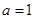 时,求证:对大于1的任意正整数
时,求证:对大于1的任意正整数 ,都有
,都有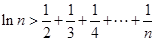 。
。
(本小题满分12分)
已知⊙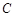 的圆心
的圆心 ,被
,被 轴截得的弦长为
轴截得的弦长为 .
.
(Ⅰ)求圆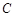 的方程;
的方程;
(Ⅱ)若圆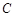 与直线
与直线 交于
交于 ,
, 两点,且
两点,且 ,求
,求 的值.
的值.
(本小题满分12分)
已知直三棱柱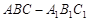 中,
中, ,
,  ,若
,若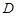 是
是 中点.
中点.
(Ⅰ)求证: ∥平面
∥平面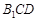 ;
;
(Ⅱ)求异面直线 和
和 所成的角.
所成的角.
(本小题满分12分)
抛物线顶点在坐标原点,焦点与椭圆 的右焦点
的右焦点 重合,过点
重合,过点 斜率为
斜率为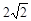 的直线与抛物线交于
的直线与抛物线交于 ,
, 两点.
两点.
(Ⅰ)求抛物线的方程;
(Ⅱ)求△ 的面积.
的面积.
(本小题满分12分)
在△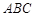 中,点
中,点 ,
,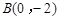 ,
,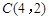 ,
,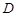 为
为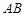 的中点,
的中点,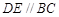 .
.
(Ⅰ)求 边上的高所在直线的方程;
边上的高所在直线的方程;
(Ⅱ)求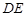 所在直线的方程.
所在直线的方程.
(本小题满分13分)
已知函数 是定义在
是定义在 上的奇函数.
上的奇函数.
(Ⅰ)求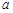 的值;
的值;
(Ⅱ)求函数 的值域;
的值域;
(Ⅲ)当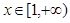 时,
时,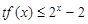 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.