(本小题满分12分)某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元,分2期或3期付款其利润为1.5万元;分4期或5期付款,其利润为2万元,用 表示经销一辆汽车的利润。
表示经销一辆汽车的利润。
| 付款方工 |
分1期 |
分2期 |
分3期 |
分4期 |
分5期 |
| 频数 |
40 |
20 |
 |
10 |
 |
(1)求上表中的 值;(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的频率P(A);(3)求
值;(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的频率P(A);(3)求 的分布列及数学期望E
的分布列及数学期望E 。
。
已知数列{an}满足:a1=20,a2=7,an+2﹣an=﹣2(n∈N*).
(Ⅰ)求a3,a4,并求数列{an}通项公式;
(Ⅱ)记数列{an}前2n项和为S2n,当S2n取最大值时,求n的值.
在 中,角
中,角 所对的边为
所对的边为 ,且满足
,且满足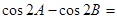

(1)求角 的值;
的值;
(2)若 且
且 ,求
,求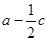 的取值范围.
的取值范围.
已知曲线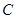 的极坐标方程是
的极坐标方程是 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 (
( 为参数).
为参数).
(Ⅰ)写出直线 的普通方程与曲线
的普通方程与曲线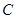 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线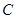 经过伸缩变换
经过伸缩变换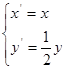 得到曲线
得到曲线 ,设
,设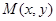 为曲线
为曲线 上任一点,求
上任一点,求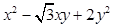 的最小值,并求相应点
的最小值,并求相应点 的坐标.
的坐标.
设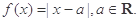
(Ⅰ)当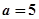 ,解不等式
,解不等式 ;
;
(Ⅱ)当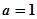 时,若
时,若
 ,使得不等式
,使得不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围.
如图,在正△ABC中,点D,E分别在边AC, AB上,且AD=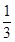 AC,AE=
AC,AE= AB,BD,CE相交于点F.
AB,BD,CE相交于点F.
(Ⅰ)求证:A,E,F,D四点共圆;
(Ⅱ)若正△ABC的边长为2,求A,E,F,D所在圆的半径.