设数列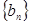 满足:
满足: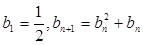 。
。
(1)求证: ;
;
(2)若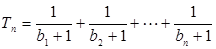 ,对任意的正整数
,对任意的正整数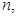
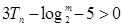 恒成立,求
恒成立,求 的取值范围。
的取值范围。
(本小题满分12分)
在△ABC中,tanA=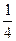
 ,tanB=
,tanB= .
.
(I)求角C的大小;
(II)若AB边的长为 ,求BC边的长
,求BC边的长
某国采用养老储备金制度.公民在就业的第一年就交纳养老储备金,数目为a1,以后每年交纳的数目均比上一年增加d(d>0),因此,历年所交纳的储务金数目a1,a2,…是一个公差为d的等差数列,与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.这就是说,如果固定年利率为r(r>0),那么,在第n年末,第一年所交纳的储备金就变为a1(1+r)a-1,第二年所交纳的储备金就变为a2(1+r)a-2,……,以Tn表示到第n年末所累计的储备金总额.
(Ⅰ)写出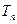 与
与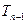 (n≥2)的递推关系式;
(n≥2)的递推关系式;
(Ⅱ)求证:Tn=An+Bn,其中{An}是一个等比数列,{Bn}是一个等差数列.
在医学生物学试验中,经常以果蝇作为试验对象,一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子:6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.以ξ表示笼内还剩下的果蝇的只数.
(Ⅰ)写出ξ的分布列(不要求写出计算过程);
(Ⅱ)求数学期望Eξ;
(Ⅲ)求概率P(ξ≥Eξ).
设a≥0,f (x)=x-1-ln2 x+2a ln x(x>0).
(Ⅰ)令F(x)=xf'(x),讨论F(x)在(0.+ )内的单调性并求极值;
)内的单调性并求极值;
(Ⅱ)求证:当x>1时,恒有x>ln2x-2a ln x+1.
如图,在六面体ABCD-A1B1C1D1中,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2.
(Ⅰ)求证:A1C1与AC共面,B1D1与BD共面;
(Ⅱ)求证:平面A1ACC1⊥平面B1BDD1;
(Ⅲ)求二面角A-BB1-C的大小(用反三角函数值表示).