由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图示:
| |
|
| 4 |
3 5 6 6 6 7 7 7 8 8 9 9 |
| 5 |
0 1 1 2 |
| |
|
指出这组数据的众数和中位数;
若视力测试结果不低于5.0,则称为“健康视力”,求校医从这16人中随机选取3人,至多有1人是“健康视力”的概率;以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记 表示抽到“健康视力”学生的人数,求
表示抽到“健康视力”学生的人数,求 的分布列及数学期望
的分布列及数学期望
(本小题满分12分)
对于函数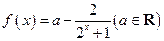 :
:
(Ⅰ) 是否存在实数 使函数
使函数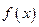 为奇函数?
为奇函数?
(Ⅱ) 探究函数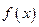 的单调性(不用证明),并求出函数
的单调性(不用证明),并求出函数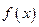 的值域.
的值域.
((本小题满分12分)
设集合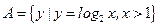 ,
,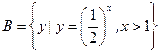 ,
,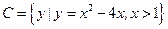 .
.
求(Ⅰ) ; (Ⅱ)
; (Ⅱ)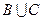 ; (Ⅲ)
; (Ⅲ)
本小题满分12分)
(Ⅰ) 已知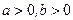 ,化简
,化简 ;
;
(Ⅱ) 已知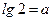 ,
, ,试用
,试用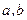 表示
表示 .
.
已知函数 (
(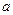 ,
, 均为正常数) .
均为正常数) .
(1)若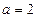 ,求函数
,求函数 在区间
在区间 上的单调减区间;
上的单调减区间;
(2)设函数在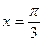 处有极值.
处有极值.
①对于一切 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围;
②若函数f (x)在区间 上是单调增函数,求实数
上是单调增函数,求实数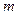 的取值范围.
的取值范围.
如图,在平面直角坐标系 中,椭圆
中,椭圆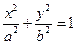
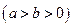 的右焦点为
的右焦点为 ,上下顶点分别为
,上下顶点分别为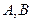 ,直线
,直线 交椭圆于
交椭圆于 点,且
点,且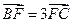 .(1)求椭圆的离心率;(2)若
.(1)求椭圆的离心率;(2)若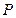 点是椭圆上弧
点是椭圆上弧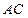 上动点,四边形
上动点,四边形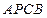 面积的最小值为
面积的最小值为 ,求椭圆的方程.
,求椭圆的方程.