在直角坐标系 中,以O为极点,
中,以O为极点, 轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为
轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为 ,曲线
,曲线 的参数方程为
的参数方程为 ,(
,(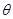 为参数,
为参数, )。
)。
(Ⅰ)求C1的直角坐标方程;
(Ⅱ)当C1与C2有两个公共点时,求实数 的取值范围。
的取值范围。
四棱锥 中,
中, ⊥底面
⊥底面 ,
, ,
, ,
, .
.
(Ⅰ)求证: ⊥平面
⊥平面 ;
;
(Ⅱ)若侧棱 上的点
上的点 满足
满足 ,求三棱锥
,求三棱锥 的体积.
的体积.
一个多面体的直观图、正视图、侧视图、俯视图如图所示,M、N分别为A1B、B1C1的中点.
(1)求证:MN//平面ACC1A1;
(2)求证:MN^平面A1BC.
如图,四棱锥 的底面是正方形,
的底面是正方形, 底面
底面 ,
, 是
是 上一点
上一点
(1)求证:平面 平面
平面 ;
;
(2)设 ,
, ,求点
,求点 到平面
到平面 的距离.
的距离.
解答下列问题:
(1)求平行于直线3x+4y 2=0,且与它的距离是1的直线方程;
(2)求垂直于直线x+3y 5=0且与点P( 1,0)的距离是 的直线方程.
的直线方程.
如图示,在底面为直角梯形的四棱椎P ABCD中,AD//BC,ÐABC= 900, PA^平面ABCD,PA= 4,AD= 2,AB=2 ,BC = 6.
,BC = 6.
(1)求证:BD^平面PAC ;
(2)求二面角A—PC—D的正切值;
(3)求点D到平面PBC的距离.