(本小题12分)如图,海中有一小岛,周围3.8海里内有暗礁。一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北端东60°。若此舰不改变舰行的方向继续前进,问此舰有没有触礁的危险?
已知全集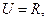 且
且 ,
, .
.
求(1)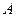 ,
,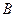 ;(2)求
;(2)求 .
.
(本题16分)已知方程x2+y2-2x-4y+m=0.
(1)若此方程表示圆,求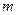 的取值范围;
的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M,N两点,且OM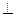 ON(O为坐标原点)求m的值;
ON(O为坐标原点)求m的值;
(3)在(2)的条件下,求以MN为直径的圆的方程.
.如图,互相垂直的两条公路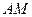 、
、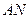 旁有一矩形花园
旁有一矩形花园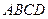 ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园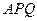 ,要求
,要求 在射线
在射线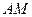 上,
上,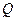 在射线
在射线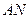 上,且
上,且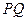 过点
过点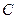 ,其中
,其中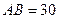 米,
米,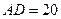 米. 记三角形花园
米. 记三角形花园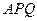 的面积为S.
的面积为S.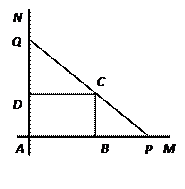
(Ⅰ)当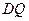 的长度是多少时,S最小?并求S的最小值.
的长度是多少时,S最小?并求S的最小值.
(Ⅱ)要使S不小于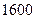 平方米,则
平方米,则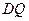 的长应在什么范围内?
的长应在什么范围内?
(本题14分)已知△ABC中,角A,B,C,所对的边分别是a,b,c,且2(a2+b2-c2)=3ab.
(1)求cosC;
(2)若c=2,求△ABC面积的最大值.
(本题14分)已知P(2,1),直线l:x-y+4=0.
(1)求过点P与直线l平行的直线方程;
(2) 求过点P与直线l垂直的直线方程.