已知10箱苹果,以每箱15千克为标准,超过15千克的数记为正数,不足15千克的数记为负数,称重记录如下:+0.2,—0.2,+0.7,—0.3,—0.4,+0.6,0,—0.1,+0.3,—0.2
(1)求10箱苹果的总重量;
(2)若每箱苹果的重量标准为10 0.5(千克),则这10箱有几箱不符合标准的?
0.5(千克),则这10箱有几箱不符合标准的?
如图,已知二次函数 的图象经过A(2,0)、B(0,-6)两点。
的图象经过A(2,0)、B(0,-6)两点。
(1)求这个二次函数的解析式
(2)设该二次函数的对称轴与 轴交于点C,连结BA、BC,求△ABC的面积。
轴交于点C,连结BA、BC,求△ABC的面积。
如图,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点)。
(1)将△ABC绕点C逆时针旋转90°,得到△CDE.写出点B对应点D和点A对应点E的坐标。
(2) 若以格点P、A、B为顶点的三角形与△CDE相似但不全等,请写出符合条件格点P的坐标。
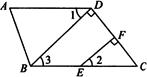
如图所示,已知BD⊥CD于D,EF⊥CD于F, ,
,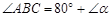 ,其中
,其中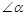 为锐角,求证:
为锐角,求证: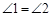 。
。
如图①②所示,将两个相同三角板的两个直角顶点O重合在一起,像图①②那样放置。
①②
(1)若∠BOC=60°,如图①,猜想∠AOD的度数。
(2)若∠BOC=70°,如图②,猜想∠AOD的度数。
(3)猜想∠AOD和∠BOC的关系,并写出理由。
完成下面的证明:已知,如图,AB∥CD,EG平分∠BEF,FG平分∠EFD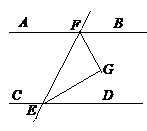
求证:∠EGF=90°
证明:∵HG∥AB(已知)∴∠1=∠3( )
又∵HG∥CD(已知)∴∠2=∠4( )
∵AB∥CD(已知)∴∠BEF+___________=180°( )
又∵EG平分∠BEF(已知)∴∠1= ∠______( )
∠______( )
又∵FG平分∠EFD(已知) ∴∠2= ∠( )
∠( )
∴∠1+∠2= (___________+______________)∴∠1+∠2=90°
(___________+______________)∴∠1+∠2=90°
∴∠3+∠4=90°( )即∠EGF=90°