商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少.把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元.现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的价格(标价)出售. 问:
(1)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(2)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
已知函数
(I)讨论函数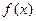 的单调性;
的单调性;
(II)设 .如果对任意
.如果对任意 ,
, ,求
,求 的取值范围。
的取值范围。
已知椭圆
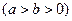 的离心率为
的离心率为 ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设 直线
直线 与椭圆
与椭圆 交于
交于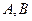 两点,且以
两点,且以 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点 ,
,
求 面积的最大值.
面积的最大值.
本着健康、低碳的生活理念,租自行车骑游的人越来越多。某自行车租车点的收费标准是每车每次租不超过两小时免费,超过两小时的收费标准为每小时2元(不足1小时的部分按1小时计算)。甲、乙独立地来该租车点租车骑游。设甲、乙不超过两小时还车的 概率分别为;
概率分别为;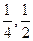 ;两小时以上且不超过三小时还车
;两小时以上且不超过三小时还车 的概率分别为
的概率分别为 ;两人租车时间都不会超过四小时。
;两人租车时间都不会超过四小时。
(Ⅰ)求出甲、乙所付租车费用相同的概率;
(Ⅱ)设甲、乙两人所付的租车费用之和为随机变量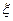 ,求
,求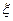 的分布列与数学期望
的分布列与数学期望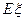 ;
;
(12 分)已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点
分)已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点
(Ⅰ)求证:BD平分∠ABC
(Ⅱ)若AB=4,AD=6,BD=8,求AH的长
某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
(1)由表中数据分析,是否有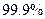 把握认为收看新闻节目的观众与年龄有关?
把握认为收看新闻节目的观众与年龄有关?
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(3)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率。
附: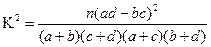
随机变量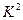 的概率分布:
的概率分布: