某商场将进价为2000元的冰箱以2400元出售,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的数量是y台,请写出y与x之间的函数关系式;(不要求写自变量的取值范围)
(2)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是z元,请写出z与x之间的函数关系式;(不要求写自变量的取值范围)
(3)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
已知抛物线 y= ax 2+ bx+ c经过 A(﹣1,0), B(4,0), C(0,﹣2)三点.
(1)请直接写出抛物线的解析式.
(2)连接 BC,将直线 BC平移,使其经过点 A,且与抛物线交于点 D,求点 D的坐标.
(3)在(2)中的线段 AD上有一动点 E(不与点 A、点 D重合),过点 E作 x轴的垂线与抛物线相交于点 F,当点 E运动到什么位置时,△ AFD的面积最大?求出此时点 E的坐标和△ AFD的最大面积.

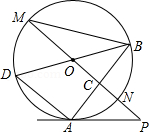
如图, PA为⊙ O的切线, A为切点,直线 PO交⊙ O于点 M、 N,过点 A作 PO的垂线 AB,垂足为 C,交⊙ O于点 B,延长 BO与⊙ O交于点 D,连接 AD、 BM.
(1)等式 OD 2= OC• OP成立吗?若成立,请加以证明;若不成立,请说明理由.
(2)若 AD=6,tan∠ M= ,求sin∠ D的值.
在我市双城同创的工作中,某社区计划对1200 m 2的区域进行绿化,经投标,由甲、乙两个施工队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为300 m 2区域的绿化时,甲队比乙队少用3天.
(1)甲、乙两施工队每天分别能完成绿化的面积是多少?
(2)设先由甲队施工 x天,再由乙队施工 y天,刚好完成绿化任务,求 y与 x的函数关系式.
(3)若甲队每天绿化费用为0.4万元,乙队每天绿化费用为0.15万元,且甲、乙两队施工的总天数不超过14天,则如何安排甲、乙两队施工的天数,使施工费用最少?并求出最少费用.
我市某中学为了深入学习社会主义核心价值观,特对本校部分学生(随机抽样)进行了一次相关知识的测试(成绩分为 A、 B、 C、 D、 E、五个组, x表示测试成绩),通过对测试成绩的分析,得到如图所示的两幅不完整的统计图,请你根据图中提供的信息解答以下问题.
A组:90≤ x≤100 B组:80≤ x<90 C组:70≤ x<80 D组:60≤ x<70 E组: x<60 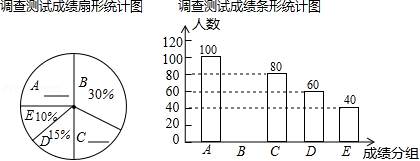
(1)参加调查测试的学生共有 人;请将两幅统计图补充完整.
(2)本次调查测试成绩的中位数落在 组内.
(3)本次调查测试成绩在80分以上(含80分)为优秀,该中学共有3000人,请估计全校测试成绩为优秀的学生有多少人?
一个不透明的口袋中装有4个球,分别是红球和白球,这些球除颜色外都相同,将球搅匀,先从中任意摸出一个球,恰好摸到红球的概率等于 .
(1)求口袋中有几个红球?
(2)先从中任意摸出一个球,从余下的球中再摸出一个球,请用列表法或树状图法求两次摸到的球中一个是红球和一个是白球的概率.