若关于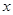 的不等式
的不等式 的解集是
的解集是 ,
, 的定义域是
的定义域是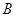 ,若
,若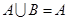 ,求实数
,求实数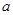 的取值范围。
的取值范围。
地为绿化环境,移栽了银杏树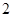 棵,梧桐树
棵,梧桐树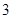 棵.它们移栽后的成活率分别
棵.它们移栽后的成活率分别
为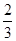 、
、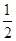 ,每棵树是否存活互不影响,在移栽的
,每棵树是否存活互不影响,在移栽的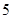 棵树中:
棵树中:
(1)求银杏树都成活且梧桐树成活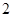 棵的概率;
棵的概率;
(2)求成活的棵树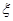 的分布列与期望.
的分布列与期望.
设函数 ,
, .
.
(1)若 ,求
,求 的最大值及相应的
的最大值及相应的 的取值集合;
的取值集合;
(2)若 是
是 的一个零点,且
的一个零点,且 ,求
,求 的值和
的值和 的最小正周期.
的最小正周期.
已知椭圆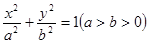 的右焦点为
的右焦点为 ,离心率
,离心率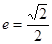 ,
,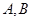 是椭圆上的动点.
是椭圆上的动点.
(1)求椭圆标准方程;
(2)若直线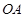 与
与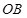 的斜率乘积
的斜率乘积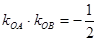 ,动点
,动点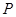 满足
满足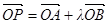 ,(其中实数
,(其中实数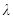 为常数).问是否存在两个定点
为常数).问是否存在两个定点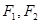 ,使得
,使得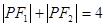 ?若存在,求
?若存在,求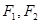 的坐标及
的坐标及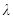 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知函数 .
.
(1)当 时,求
时,求 的极值;
的极值;
(2)若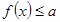 对
对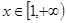 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
如图,已知长方形 中,
中, ,
,  ,
,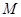 为
为 的中点.将
的中点.将 沿
沿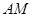 折起,使得平面
折起,使得平面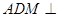 平面
平面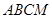 .
.
(1)求证: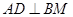 ;
;
(2)若点 是线段
是线段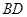 的中点,求二面角
的中点,求二面角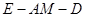 的余弦值.
的余弦值.