地为绿化环境，移栽了银杏树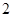
棵，梧桐树
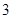棵.它们移栽后的成活率分别
为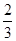
、
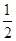，每棵树是否存活互不影响，在移栽的
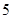棵树中：
（1）求银杏树都成活且梧桐树成活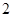棵的概率；
（2）求成活的棵树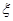
的分布列与期望.
对400个某种型号的电子元件进行寿命追踪调查，其频率分布表如下表：
| 寿命（h） |
频率 |
| 500600 |
0.10 |
| 600700 |
0.15 |
| 700800 |
0.40 |
| 800900 |
0.20 |
| 9001000 |
0.15 |
| 合计 |
1 |
（I）在下图中补齐频率分布直方图；
（II）估计元件寿命在500800h以内的概率。
在直角坐标系xoy中，直线
的参数方程为
（t为参数）。在极坐标系（与直角坐标系xoy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为
。
（Ⅰ）求圆C的直角坐标方程；
（Ⅱ）设圆C与直线交于点A、B，若点P的坐标为
，求|PA|+|PB|。
已知函数
.
（Ⅰ）求
的最小值；
（Ⅱ）若对所有
都有
，求实数
的取值范围.
某商场准备在五一劳动节期间举行促销活动，根据市场调查，该商场决定从3种服装商品、2种家电商品、4种日用商品中，选出3种商品进行促销活动.
（Ⅰ）试求选出的3种商品中至少有一种日用商品的概率；
（Ⅱ）商场对选出的A商品采用的促销方案是有奖销售，即在该商品现价的基础上将价格提高90元，同时允许顾客有3次抽奖的机会，若中奖，则每次中奖都可获得一定数额的奖金.假设顾客每次抽奖时获奖与否是等可能的，请问：商场应将中奖奖金数额最高定为多少元，才能使促销方案对自己有利？
如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(Ⅰ) 证明：PA⊥BD；
(Ⅱ) 若PD=AD，求二面角A-PB-C的余弦值。