已知p:|x-3|≤2,q:(x-m+1)(x-m-1)≤0,若﹁p是﹁q的充分而不必要条件,求实数m的取值范围.
用秦九韶算法求多项式 ,当x=2时的值.
,当x=2时的值.
过曲线 上的一点
上的一点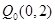 作曲线的切线,交x轴于点P1,过P1作垂直于x轴的直线交曲线于Q1,过Q1作曲线的切线,交x轴于点P2;过P2作垂直于x轴的直线交曲线于Q2,过Q2作曲线的切线
作曲线的切线,交x轴于点P1,过P1作垂直于x轴的直线交曲线于Q1,过Q1作曲线的切线,交x轴于点P2;过P2作垂直于x轴的直线交曲线于Q2,过Q2作曲线的切线 ,交x轴于点P3;……如此继续下去得到点列:
,交x轴于点P3;……如此继续下去得到点列: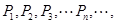 设
设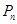 的横坐标为
的横坐标为
(I)试用n表示 ;
;
(II)证明: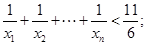
(III)证明: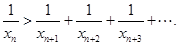
已知椭圆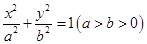 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线 是抛物线
是抛物线 的一条切线.
的一条切线.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点 的动直线L交椭圆C
的动直线L交椭圆C 于 A.B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ? 若存在,求点T坐标;若不存在,说明理
于 A.B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ? 若存在,求点T坐标;若不存在,说明理 由.
由.
已知曲线 在
在 点
点 处的切线斜率为
处的切线斜率为
(Ⅰ)求 的极值;
的极值;
(Ⅱ)设 在(一∞,1)上是增函数,求实数
在(一∞,1)上是增函数,求实数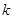 的取值范围
的取值范围