(本小题满分14分)
已知函数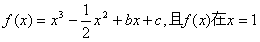 处取得极值.
处取得极值.
(Ⅰ)求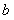 的值;
的值;
(Ⅱ)若当 恒成立,求
恒成立,求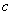 的取值范围;
的取值范围;
(Ⅲ)对任意的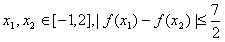 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
设函数 ,其中
,其中 ;
;
(1)若 的最小正周期为
的最小正周期为 ,求
,求 的单调增区间;
的单调增区间;
(2)若函数 的图象的一条对称轴为
的图象的一条对称轴为 ,求
,求 的值.
的值.
已知集合 ,
,
集合 ,
,
 ,
,
求实数 的取值范围.
的取值范围.
(本小题满分14分)
已知函数f (x)=ex,g(x)=lnx,h(x)=kx+b.
(1)当b=0时,若对 x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
(2)设h(x)的图象为函数f (x)和g(x)图象的公共切线,切点分别为(x1, f (x1))和(x2, g(x2)),其中x1>0.
①求证:x1>1>x2;
②若当x≥x1时,关于x的不等式ax2-x+xe +1≤0恒成立,求实数a的取值范围.
+1≤0恒成立,求实数a的取值范围.
(本小题满分14分)
已知椭圆的中心是坐标原点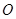 ,焦点在x轴上,离心率为
,焦点在x轴上,离心率为 ,又椭圆上任一点到两焦点的距离和为
,又椭圆上任一点到两焦点的距离和为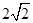 ,过点M(0,
,过点M(0, )与x轴不垂直的直线
)与x轴不垂直的直线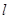 交椭圆于P、Q两点.
交椭圆于P、Q两点.
(1)求椭圆的方程;
(2)在y轴上是否存在定点N,使以PQ为直径的圆恒过这个点?若存在,求出N的坐标,若不存在,说明理由.
(本小题满分13分)
已知数列{an}的首项a1=" t" >0, ,n=1,2,……
,n=1,2,……
(1)若t =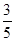 ,求
,求 是等比数列,并求出{an}的通项公式;
是等比数列,并求出{an}的通项公式;
(2)若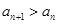 对一切
对一切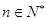 都成立,求t的取值范围.
都成立,求t的取值范围.