(本小题满分14分)
已知点(1, )是函数
)是函数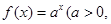 且
且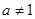 )的图象上一点,等比数列
)的图象上一点,等比数列 的前
的前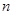 项和为
项和为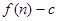 ,数列
,数列
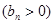 的首项为
的首项为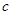 ,且前
,且前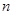 项和
项和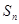 满足
满足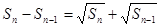 (
(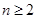 ).
).
(1)求数列 和
和 的通项公式;
的通项公式;
(2)若数列{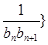 前
前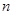 项和为
项和为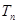 ,问
,问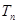 >
>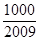 的最小正整数
的最小正整数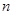 是多少?
是多少?
已知全集U=R,集合M={x|x≤a-2或x≥a+3},N={x|-1≤x≤2}.
(1)若 ,求(
,求( )∩(
)∩( );
);
(2)若 ∩
∩ =
= ,求实数
,求实数 的取值范围.
的取值范围.
已知函数 ,
, .
.
(Ⅰ)若函数 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅱ)设直线 为函数
为函数 的图象上一点
的图象上一点 处的切线.证明:在区间
处的切线.证明:在区间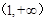 上存在唯一的
上存在唯一的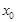 ,使得直线
,使得直线 与曲线
与曲线 相切.
相切.
等差数列 中,
中,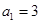 ,前
,前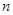 项和为
项和为 ,等比数列
,等比数列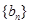 各项均为正数,
各项均为正数,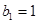 ,且
,且 ,
,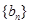 的公比
的公比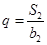
(1)求 与
与 ;
;
(2)证明:
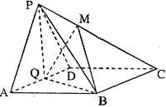
如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形,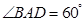 ,
,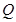 为
为 的中点。
的中点。
(1)若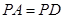 ,求证:平面
,求证:平面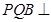 平面
平面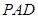 ;
;
(2)点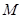 在线段
在线段 上,
上, ,试确定
,试确定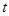 的值,使
的值,使 平面
平面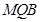 ;
; (3)在(2)的条件下,若平面
(3)在(2)的条件下,若平面 平面ABCD,且
平面ABCD,且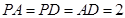 ,求二面角
,求二面角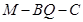 的大小。
的大小。
已知集合 ,集合
,集合
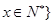 ,集合
,集合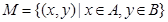
(1)求从集合 中任取一个元素是(3,5)的概率;
中任取一个元素是(3,5)的概率;
(2)从集合 中任取一个元素,求
中任取一个元素,求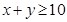 的概率;
的概率;
(3)设 为随机变量,
为随机变量,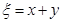 ,写出
,写出 的分布列,并求
的分布列,并求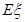 。
。