(本小题12分)如图,甲船以每小时30 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
袋中装有大小相同的10个球,其中5个白球,3个红球,2个黑球,现在依次从中取出3个球。(Ⅰ)求取出的3个球不是同一种颜色的概率;(Ⅱ)求取出的3个球中所含红球的个数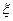 的分布列及期望。
的分布列及期望。
已知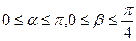 ,且
,且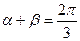 .
.
求: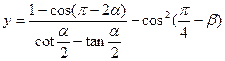 的最大值,并求出相应的
的最大值,并求出相应的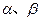 的值.
的值.
设函数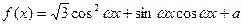 (其中
(其中 >0,
>0, ),且
),且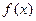 的图象在y轴右侧的第一个高点的横坐标为
的图象在y轴右侧的第一个高点的横坐标为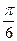 .(1)求
.(1)求 的值;(2)如果
的值;(2)如果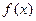 在区间
在区间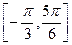 上的最小值为
上的最小值为 ,求a的值.
,求a的值.
设函数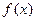 是定义在区间
是定义在区间 上以2为周期的函数,记
上以2为周期的函数,记 .已知当
.已知当 时,
时, ,如图.
,如图.
(1)求函数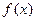 的解析式;
的解析式;
(2)对于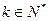 ,求集合
,求集合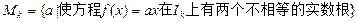 .
.
(本小题14分)已知函数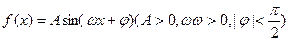 在一个周期内的图象下图所示。(1)求函数的解析式;(2)设
在一个周期内的图象下图所示。(1)求函数的解析式;(2)设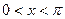 ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围和这两个根的和。
有两个不同的实数根,求实数m的取值范围和这两个根的和。