如图，A、B两座城市相距100千米，现计划在两城市间修筑一条高速公路（即线段AB）．经测量，森林保护区中心P点既在A城市的北偏东30°的方向上，又在B城市的南偏东45°的方向上．已知森林保护区的范围是以P为圆心，35千米为半径的圆形区域内．请问：计划修筑的这条高速公路会不会穿越森林保护区？请通过计算说明．
（参考数据：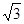
≈1.732，
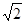≈1.414）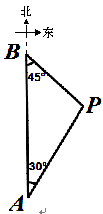
如图, 已知抛物线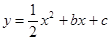
与y轴相交于C，与x轴相交于A、B，点A的坐标为（2，0），点C的坐标为（0，-1）．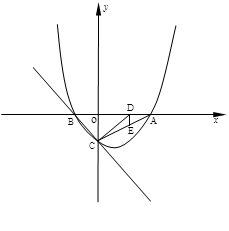
（1）求抛物线的解析式；
（2）点E是线段AC上一动点，过点E作DE⊥x轴于点D，连结DC，当△DCE的面积最大时，求点D的坐标；
（3）在直线BC上是否存在一点P，使△ACP为以AC为腰的等腰三角形，若存在，求点P的坐标，若不存在，说明理由．
如图一次函数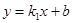
的图象与反比例函数
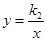的图象交于点A
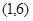，B（3，a）．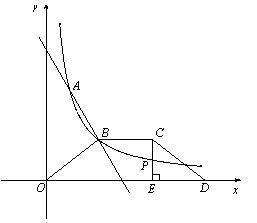
（1）求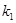
、
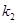的值；
（2）直接写出一次函数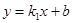的值大于反比例函数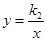的值时x的取值范围：
；
（3）如图，等腰梯形OBCD中，BC//OD，OB=CD，OD边在x 轴上，过点C作CE⊥OD于点E，CE和反比例函数的图象交于点P，当点P为CE的中点时，求梯形OBCD的面积．
为发展旅游经济．我市某景区对门票采用灵活的售票方法吸引游客．门票定价为50元/人．非节假日打a折售票．节假日按团队人数分段定价售票，即m人以下(含m人)的团队接原价售票；超过m人的团队．其中m人仍按原价售票．超过m人部分的游客打b折售票．设某旅游团人数为x人．非节假日购票款为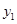
(元)，节假日购票款为
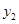(元)．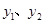
与x之间的函数图象如图所示．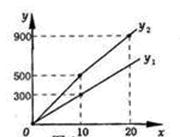
（1）观察图象可知：a=______；b=______；m=______；
（2）直接写出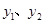与x之间的函数关系式：
（3）某旅行导游王娜于5月1日带A团．5月20日(非节假日)带B团都到该景区旅游．共付门票款1900元．A， B两个团队合计50人，求A，B两个团队各有多少人?
某工厂计划生产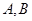
两种产品共10件，其生产成本和利润如下表：
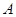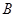 种产品 |
 种产品 |
|
| 成本（万元∕件） |
3 |
5 |
| 利润（万元∕件） |
1 |
2 |
（1）若工厂计划获利14万元，问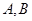两种产品应分别生产多少件？
（2）若工厂投入资金不多于44万元，且获利多于14万元，问工厂有哪几种生产方案？哪种方案获利最大？并求最大利润.