设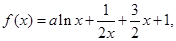 其中
其中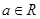 ,曲线
,曲线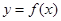 在点
在点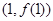 处的切线垂直于
处的切线垂直于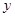 轴.
轴.
(Ⅰ) 求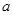 的值;
的值;
(Ⅱ) 求函数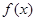 的极值.
的极值.
(本小题12分)
已知双曲线的中心在原点,左右焦点分别为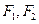 ,离心率为
,离心率为 ,且过点
,且过点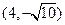 ,
,
(1)求此双曲线的标准方程;
(2)若直线系 (其中
(其中 为参数)所过的定点
为参数)所过的定点 恰在双曲线上,求证:
恰在双曲线上,求证: 。
。
(本小题12分)
如图所示,直 三棱柱ABC—A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
三棱柱ABC—A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
(1)求 的长;
的长;
(2)求cos< >的值;
>的值;
](3)求证:A1B⊥C1M.
(本小题满分14分)
已知二次函数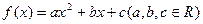 ,且同时满足下列条件:
,且同时满足下列条件:
①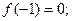 ② 对任意的实数
② 对任意的实数 ,都有
,都有
③ 当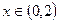 时,有
时,有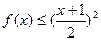 。
。
(1)求 ;
;
(2)求 的值;
的值;
(3)当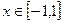 时,函数
时,函数 是单
是单 调函数,求
调函数,求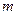 的取值范围。
的取值范围。
(本小题满分12分)
已知数列
⑴求出 ;
;
⑵猜想前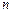 项和
项和 并证明
并证明
本小题满分12分)
已知f(x)= (a>0,a≠1)
(a>0,a≠1)
1.求f(x)的定义域;
2.若f(x)>0,求x的取值范围。