某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如右图所示.
(1)下表是年龄的频数分布表,求正整数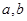 的值;
的值;
| 区间 |
[25,30) |
[30,35) |
[35,40) |
[40,45) |
[45,50] |
| 人数 |
50 |
50 |
 |
150 |
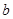 |
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
设等差数列 的前
的前 项和为
项和为 ,满足:
,满足: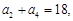
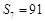 .递增的等比数列
.递增的等比数列 前
前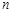 项和为
项和为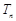 ,满足:
,满足: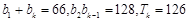 .
.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)设数列 对
对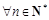 ,均有
,均有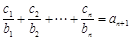 成立,求
成立,求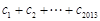 .
.
已知向量 ,
,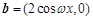
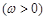 ,函数
,函数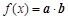 的图象与直线
的图象与直线 的相邻两个交点之间的距离为
的相邻两个交点之间的距离为 .
.
(Ⅰ)求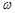 的值;
的值;
(Ⅱ)求函数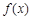 在
在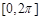 上的单调递增区间.
上的单调递增区间.
下面四个图案,都是由小正三角形构成,设第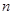 个图形中有
个图形中有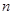 个正三角形中所有小正三角形边上黑点的总数为
个正三角形中所有小正三角形边上黑点的总数为 .
.
图1图2图3图4
(Ⅰ)求出 ,
,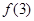 ,
,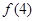 ,
, ;
;
(Ⅱ)找出 与
与 的关系,并求出
的关系,并求出 的表达式;
的表达式;
(Ⅲ)求证: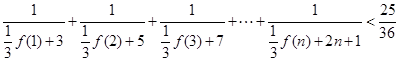 (
( ).
).
设函数 ,若
,若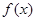 在点
在点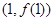 处的切线斜率为
处的切线斜率为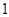 .
.
(Ⅰ)用 表示
表示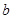 ;
;
(Ⅱ)设 ,若
,若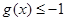 对定义域内的
对定义域内的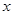 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
设 的内角
的内角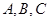 所对的边长分别为
所对的边长分别为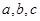 ,且满足
,且满足
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,
, 边上的中线
边上的中线 的长为
的长为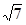 ,求
,求 的面积.
的面积.