(本题满分12分)在如图的多面体中,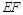 ⊥平面
⊥平面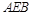 ,
, ,
,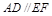 ,
,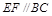 ,
,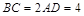 ,
, ,
, ,
, 是
是 的中点.
的中点.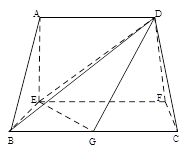
(Ⅰ) 求证: 平面
平面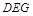 ;
;
(Ⅱ) 求证: ;
;
(Ⅲ) 求二面角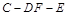 的余弦值.
的余弦值.
(本小题满分12分)某班 50名学生在一模数学考试中,成绩都属于区间[60,110]。将成绩按如下方式分成五组:第一组[60,70);第二组[70,80);第三组[80,90);第四组[90,100);第五组[100,110]。部分频率分布直方图如图3所示,及格(成绩不小于90分)的人数为20。
50名学生在一模数学考试中,成绩都属于区间[60,110]。将成绩按如下方式分成五组:第一组[60,70);第二组[70,80);第三组[80,90);第四组[90,100);第五组[100,110]。部分频率分布直方图如图3所示,及格(成绩不小于90分)的人数为20。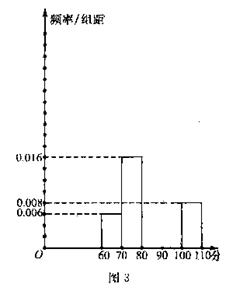
(1)请补全频率分布直方图;
(2)在成绩属于[60,70)∪[100,110]的学生中任取
两人,成绩记为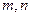 ,求
,求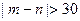 的概率;
的概率;
(本小题满分12分)如图所示,已知矩形ABCD中,AB=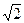 ,AD=1,将△ABD沿BD折起,使点A在平面BCD内的射影落在DC上
,AD=1,将△ABD沿BD折起,使点A在平面BCD内的射影落在DC上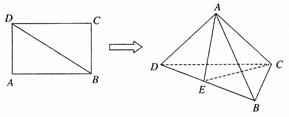
(1)求证:平面ADC⊥平面BCD;
(2)求点C到平面ABD的距离;
(3)若E为BD中点,求二面角B—AD—E的大小。
(本小题满分12分)已知在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点。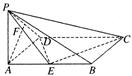
(1)求证:AF//平面PEC;
(2)求PC与平面ABCD所成的角的大小;
(3)求二面角P—EC—D的大小。
(本小题满分12分)如图所示,在直三棱柱ABC—A1B1C1中,AB=1,AC=AA1=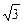 ,∠ABC=60°.
,∠ABC=60°.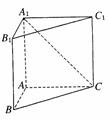
(1)求证:AB⊥A1C;w
(2)求二面角A—A1C—B的余弦值。
(本小题满分12分)在直三棱柱ABC-A 1B 1C 1中,∠ABC=90°,AB=BC=1,AA 1=2。 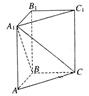 (1)求异面直线B 1C 1与AB所成角的大小;
(1)求异面直线B 1C 1与AB所成角的大小;
(2)求B 1C 1与平面A 1BC的距离。