(本小题满分12分)某班从6名班干部中(男生4人,女生2人)选3人参加学校义务劳动;(1)求男生甲或女生乙被选中的概率;
(2)在男生甲被选中的情况下,求女生乙也被选中的概率;
(3)设所选3人中女生人数为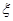 ,求
,求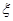 的分布列及数学期望。
的分布列及数学期望。
如图,在四棱锥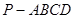 中,底面
中,底面 为矩形,
为矩形,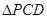 为等边三角形,
为等边三角形,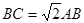 ,点
,点 为
为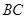 中点,平面
中点,平面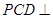 平面
平面 .
.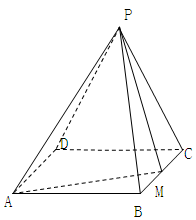
(1)求异面直线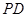 和
和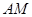 所成角的余弦值;
所成角的余弦值;
(2)求二面角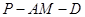 的大小.
的大小.
已知椭圆C: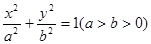 的左、右焦点分别为
的左、右焦点分别为 ,离心率
,离心率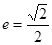 ,连接椭圆的四个顶点所得四边形的面积为
,连接椭圆的四个顶点所得四边形的面积为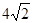 .
.
(1)求椭圆C的标准方程;
(2)设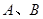 是直线
是直线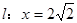 上的不同两点,若
上的不同两点,若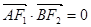 ,求
,求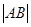 的最小值.
的最小值.
已知命题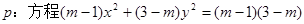 表示的曲线是双曲线;命题
表示的曲线是双曲线;命题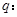 函数
函数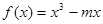 在区间
在区间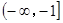 上为增函数,若“
上为增函数,若“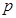
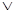
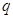 ”为真命题,“
”为真命题,“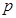

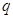 ”为假命题,求实数
”为假命题,求实数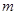 的取值范围.
的取值范围.
如图,在底面为平行四边形的四棱锥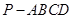 中,
中,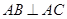 ,
, 平面
平面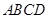 ,且
,且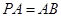 ,点
,点 是
是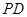 的中点.
的中点.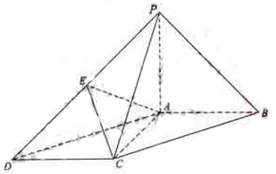
(1)求证: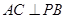 ;
;
(2)求证: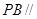 平面
平面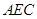 ;
;
(3)求二面角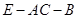 的大小.
的大小.
养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为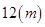 ,高
,高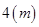 ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大
,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大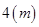 (高不变);二是高度增加
(高不变);二是高度增加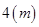 (底面直径不变)。
(底面直径不变)。
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积(地面无需用材料);
(3)哪个方案更经济些?