(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: (
( 是参数).
是参数).
(I)将曲线C的极坐标方程和直线 参数方程转化为普通方程;
参数方程转化为普通方程;
(II)若直线l与曲线C相交于A、B两点,且 ,试求实数
,试求实数 值.
值.
某初级中学共有学生2 000名,各年级男、女生人数如下表:
(1)已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.求x的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3)已知y≥245,z≥245,求初三年级中女生比男生多的概率.
某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
(1) 问各班被抽取的学生人数各为多少人?
(2) 在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率.
(3) 求平均成绩.
设关于 的一元二次方程
的一元二次方程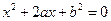 ,若
,若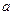 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数,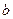 是从0,1,2三个数中任取的一个数,求上述方程有实数根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实数根的概率;
.在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相同数字的概率;
(2)求取出的两个球上标号之积能被3整除的概率.
.任意投掷两枚骰子,计算:(1)出现点数相同的概率;(2)出现点数和为奇数的概率、